19 Ενώσεις

19.1 Εισαγωγή

Είναι σπάνιο μία ανάλυση δεδομένων να περιλαμβάνει μόνο ένα πλαίσιο δεδομένων. Συνήθως έχετε πολλά πλαίσια δεδομένων και πρέπει να τα ενώσετε για να απαντήσετε στις ερωτήσεις που σας ενδιαφέρουν. Αυτό το κεφάλαιο θα σας παρουσιάσει δύο σημαντικούς τύπους ενώσεων:

Ενώσεις αλλαγής, οι οποίες προσθέτουν νέες μεταβλητές σε ένα πλαίσιο δεδομένων, οι οποίες προέρχονται από αντιστοιχισμένες παρατηρήσεις σε ένα άλλο πλαίσιο δεδομένων.
Ενώσεις φιλτραρίσματος (filtering joins), οι οποίες φιλτράρουν τις παρατηρήσεις από ένα πλαίσιο δεδομένων με βάση το αν ταιριάζουν ή όχι με μία παρατήρηση σε ένα άλλο.

Θα ξεκινήσουμε συζητώντας τα κλειδιά, τις μεταβλητές που χρησιμοποιούνται για να συνδέσουν ένα ζεύγος πλαισίων δεδομένων σε μία ένωση. Θα εδραιώσουμε τη θεωρία εξετάζοντας τα κλειδιά στα σύνολα δεδομένων του πακέτου nycflights13 και, στη συνέχεια, χρησιμοποιούμε αυτή τη γνώση για να αρχίσουμε να ενώνουμε πλαίσια δεδομένων μεταξύ τους. Στη συνέχεια θα συζητήσουμε το πώς λειτουργούν οι ενώσεις, εστιάζοντας στη δράση τους στις γραμμές. Τέλος, Θα ολοκληρώσουμε με μία συζήτηση για ενώσεις που δεν είναι ισοδύναμες, μία οικογένεια ενώσεων που παρέχουν έναν πιο ευέλικτο τρόπο αντιστοίχισης κλειδιών από την προεπιλεγμένη σχέση ισότητας.

19.1.1 Προαπαιτούμενα

Σε αυτό το κεφάλαιο, θα εξερευνήσουμε τα πέντε σχετικά σύνολα δεδομένων από το nycflights13 χρησιμοποιώντας τις συναρτήσεις ένωσης (join) της dplyr.

library(tidyverse)
library(nycflights13)

19.2 Κλειδιά

Για να κατανοήσετε τις ενώσεις, πρέπει πρώτα να κατανοήσετε πώς δύο πίνακες μπορούν να συνδεθούν μέσω ενός ζεύγους κλειδιών, που υπάρχουν σε κάθε πίνακα. Σε αυτήν την ενότητα, θα μάθετε για τους δύο τύπους κλειδιών και θα δείτε παραδείγματα και των δύο στα σύνολα δεδομένων του πακέτου nycflights13. Θα μάθετε επίσης πώς να ελέγχετε ότι τα κλειδιά σας είναι έγκυρα και τι να κάνετε εάν ο πίνακας σας δεν διαθέτει κλειδί.

19.2.1 Πρωτεύοντα και δευτερεύοντα (ξένα) κλειδιά

Κάθε ένωση περιλαμβάνει ένα ζεύγος κλειδιών: ένα πρωτεύον (ή κύριο) κλειδί και ένα ξένο (ή δευτερεύον) κλειδί. Ένα πρωτεύον κλειδί είναι μία μεταβλητή ή ένα σύνολο μεταβλητών που προσδιορίζει μοναδικά κάθε παρατήρηση. Όταν χρειάζονται περισσότερες από μία μεταβλητές, το κλειδί ονομάζεται σύνθετο κλειδί. Για παράδειγμα, στο nycflights13:

Το πλαίσιο δεδομένων airlines καταγράφει για κάθε αεροπορική εταιρεία δύο στοιχεία: τον κωδικό της εταιρείας και το πλήρες όνομά της. Μπορείτε να προσδιορίσετε μία αεροπορική εταιρεία με τον κωδικό δύο γραμμάτων που της αντιστοιχεί, καθιστώντας τη μεταβλητή carrier το πρωτεύον κλειδί.
```
airlines
#> # A tibble: 16 × 2
#>   carrier name                    
#>   <chr>   <chr>                   
#> 1 9E      Endeavor Air Inc.       
#> 2 AA      American Airlines Inc.  
#> 3 AS      Alaska Airlines Inc.    
#> 4 B6      JetBlue Airways         
#> 5 DL      Delta Air Lines Inc.    
#> 6 EV      ExpressJet Airlines Inc.
#> # ℹ 10 more rows
```

Το airports καταγράφει δεδομένα για κάθε αεροδρόμιο. Μπορείτε να προσδιορίσετε κάθε αεροδρόμιο με τον κωδικό τριών γραμμάτων που του αντιστοιχεί, καθιστώντας τη μεταβλητή faa το πρωτεύον κλειδί.

airports
#> # A tibble: 1,458 × 8
#>   faa   name                            lat   lon   alt    tz dst  
#>   <chr> <chr>                         <dbl> <dbl> <dbl> <dbl> <chr>
#> 1 04G   Lansdowne Airport              41.1 -80.6  1044    -5 A    
#> 2 06A   Moton Field Municipal Airport  32.5 -85.7   264    -6 A    
#> 3 06C   Schaumburg Regional            42.0 -88.1   801    -6 A    
#> 4 06N   Randall Airport                41.4 -74.4   523    -5 A    
#> 5 09J   Jekyll Island Airport          31.1 -81.4    11    -5 A    
#> 6 0A9   Elizabethton Municipal Airpo…  36.4 -82.2  1593    -5 A    
#> # ℹ 1,452 more rows
#> # ℹ 1 more variable: tzone <chr>

Το planes καταγράφει δεδομένα για κάθε αεροπλάνο. Μπορείτε να προσδιορίσετε ένα αεροπλάνο με τον αναγνωριστικό κωδικό του, καθιστώντας τη μεταβλητή tailnum το πρωτεύον κλειδί.

planes
#> # A tibble: 3,322 × 9
#>   tailnum  year type              manufacturer    model     engines
#>   <chr>   <int> <chr>             <chr>           <chr>       <int>
#> 1 N10156   2004 Fixed wing multi… EMBRAER         EMB-145XR       2
#> 2 N102UW   1998 Fixed wing multi… AIRBUS INDUSTR… A320-214        2
#> 3 N103US   1999 Fixed wing multi… AIRBUS INDUSTR… A320-214        2
#> 4 N104UW   1999 Fixed wing multi… AIRBUS INDUSTR… A320-214        2
#> 5 N10575   2002 Fixed wing multi… EMBRAER         EMB-145LR       2
#> 6 N105UW   1999 Fixed wing multi… AIRBUS INDUSTR… A320-214        2
#> # ℹ 3,316 more rows
#> # ℹ 3 more variables: seats <int>, speed <int>, engine <chr>

Το weather καταγράφει δεδομένα για τον καιρό στο αεροδρόμιο αναχώρησης. Μπορείτε να προσδιορίσετε κάθε παρατήρηση από το συνδυασμό τοποθεσίας και ώρας, καθιστώντας τις μεταβλητές origin και time_hour το σύνθετο πρωτεύον κλειδί.

weather
#> # A tibble: 26,115 × 15
#>   origin  year month   day  hour  temp  dewp humid wind_dir
#>   <chr>  <int> <int> <int> <int> <dbl> <dbl> <dbl>    <dbl>
#> 1 EWR     2013     1     1     1  39.0  26.1  59.4      270
#> 2 EWR     2013     1     1     2  39.0  27.0  61.6      250
#> 3 EWR     2013     1     1     3  39.0  28.0  64.4      240
#> 4 EWR     2013     1     1     4  39.9  28.0  62.2      250
#> 5 EWR     2013     1     1     5  39.0  28.0  64.4      260
#> 6 EWR     2013     1     1     6  37.9  28.0  67.2      240
#> # ℹ 26,109 more rows
#> # ℹ 6 more variables: wind_speed <dbl>, wind_gust <dbl>, …

Ένα ξένο κλειδί είναι μία μεταβλητή (ή σύνολο μεταβλητών) που αντιστοιχεί στο πρωτεύον κλειδί από έναν άλλο πίνακα. Για παράδειγμα:

Η μεταβλητή flights$tailnum είναι ένα ξένο κλειδί που αντιστοιχεί στο πρωτεύον κλειδί planes$tailnum.
Η μεταβλητή flights$carrier είναι ένα ξένο κλειδί που αντιστοιχεί στο πρωτεύον κλειδί airlines$carrier.
Η μεταβλητή flights$origin είναι ένα ξένο κλειδί που αντιστοιχεί στο πρωτεύον κλειδί airports$faa.
Η μεταβλητή flights$dest είναι ένα ξένο κλειδί που αντιστοιχεί στο πρωτεύον κλειδί airports$faa.
Η μεταβλητή flights$origin-flights$time_hour είναι ένα σύνθετο ξένο κλειδί που αντιστοιχεί στο σύνθετο πρωτεύον κλειδί weather$origin-weather$time_hour.

Αυτές οι σχέσεις συνοψίζονται και οπτικά στο Σχήμα 19.1.

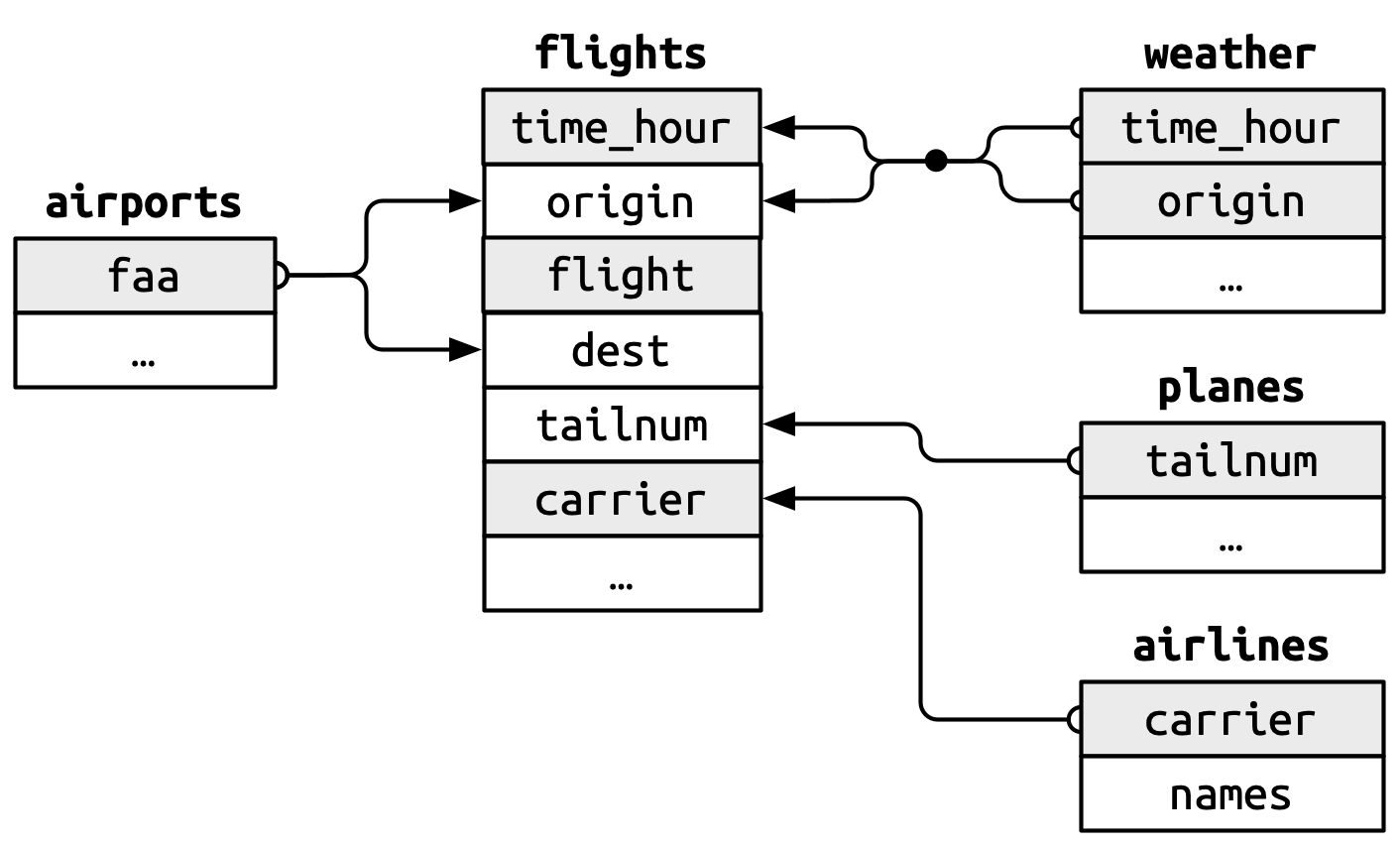
Οι σχέσεις μεταξύ αεροδρομίων, αεροπλάνων, πτήσεων, καιρού και συνόλων δεδομένων αεροπορικών εταιρειών από το πακέτο nycflights13. Η airports$faa συνδέεται με τις flights$origin και flights$dest. Η planes$tailnum συνδέεται με τη flights$tailnum. Οι weather$time_hour weather$origin συνδέονται από κοινού με τις flights$time_hour και τις flights$origin. Η airlines$carrier είναι συνδεδεμένη με τη flights$carrier. Δεν υπάρχουν απευθείας συνδέσεις μεταξύ αεροδρομίων, αεροπλάνων, αεροπορικών εταιρειών και πλαισίων δεδομένων για τον καιρό. — Σχήμα 19.1: Συνδέσεις μεταξύ και των πέντε πλαισίων δεδομένων στο πακέτο nycflights13. Οι μεταβλητές που αποτελούν ένα πρωτεύον κλειδί έχουν γκρι χρώμα, και συνδέονται με τα αντίστοιχα ξένα κλειδιά τους με βέλη.

Θα παρατηρήσετε ένα ωραίο χαρακτηριστικό στο σχεδιασμό αυτών των κλειδιών: το πρωτεύον και το ξένο κλειδί έχουν σχεδόν πάντα τα ίδια ονόματα, κάτι που, όπως θα δείτε σύντομα, θα κάνει πολύ πιο εύκολη τη ζωή σας όταν κάνετε ενώσεις. Αξίζει επίσης να σημειωθεί και η αντίθετη σχέση: σχεδόν κάθε όνομα μεταβλητής που χρησιμοποιείται σε πολλούς πίνακες έχει την ίδια σημασία σε κάθε μέρος. Υπάρχει μόνο μία εξαίρεση: η μεταβλητή year υποδηλώνει το έτος αναχώρησης στο πλαίσιο δεδομένων flights το έτος του κατασκευαστή στο πλαίσιο δεδομένων planes. Αυτό θα γίνει σημαντικό όταν αρχίσουμε να ενώνουμε πίνακες μαζί.

19.2.2 Έλεγχος πρωτευόντων κλειδιών

Τώρα που προσδιορίσαμε τα κύρια κλειδιά σε κάθε πίνακα, είναι καλή πρακτική να επαληθεύσουμε ότι όντως προσδιορίζουν μοναδικά κάθε παρατήρηση. Ένας τρόπος για να γίνει αυτό είναι να μετρώντας τις τιμές που αντιστοιχούν στα κύρια κλειδιά με την count() και να εστιάσουμε σε παρατηρήσεις όπου το πλήθος τιμών (n) είναι μεγαλύτερο από ένα. Αυτός ο έλεγχος αποκαλύπτει ότι οι μεταβλητές planes και weather δείχνουν και οι δύο καλά:

planes |> 
  count(tailnum) |> 
  filter(n > 1)
#> # A tibble: 0 × 2
#> # ℹ 2 variables: tailnum <chr>, n <int>

weather |> 
  count(time_hour, origin) |> 
  filter(n > 1)
#> # A tibble: 0 × 3
#> # ℹ 3 variables: time_hour <dttm>, origin <chr>, n <int>

Θα πρέπει επίσης να ελέγξετε για την ύπαρξη κενών τιμών στα κύρια κλειδιά σας — εάν λείπει μία τιμή, αυτό σημαίνει ότι μία παρατήρηση δεν μπορεί να αναγνωριστεί!

planes |> 
  filter(is.na(tailnum))
#> # A tibble: 0 × 9
#> # ℹ 9 variables: tailnum <chr>, year <int>, type <chr>, manufacturer <chr>,
#> #   model <chr>, engines <int>, seats <int>, speed <int>, engine <chr>

weather |> 
  filter(is.na(time_hour) | is.na(origin))
#> # A tibble: 0 × 15
#> # ℹ 15 variables: origin <chr>, year <int>, month <int>, day <int>,
#> #   hour <int>, temp <dbl>, dewp <dbl>, humid <dbl>, wind_dir <dbl>, …

19.2.3 Υποκατάστατα κλειδιά

Μέχρι στιγμής δεν έχουμε μιλήσει για το πρωτεύον κλειδί στο πλαίσιο δεδομένων flights. Δεν είναι πολύ σημαντικό εδώ, επειδή δεν υπάρχουν πλαίσια δεδομένων που να το χρησιμοποιούν ως ξένο κλειδί, αλλά παραμένει χρήσιμο να το αναφέρουμε γιατί είναι πιο εύκολο να εργαστούμε με παρατηρήσεις, αν έχουμε κάποιο τρόπο να τις περιγράψουμε σε άλλους.

Μετά από λίγη σκέψη και πειραματισμό, αποφασίσαμε ότι υπάρχουν τρεις μεταβλητές που μαζί προσδιορίζουν μοναδικά κάθε πτήση:

flights |> 
  count(time_hour, carrier, flight) |> 
  filter(n > 1)
#> # A tibble: 0 × 4
#> # ℹ 4 variables: time_hour <dttm>, carrier <chr>, flight <int>, n <int>

Κάνει αυτόματα η απουσία διπλότυπων τιμών τον συνδυασμό time_hour-carrier-flight ένα πρωτεύον κλειδί; Είναι σίγουρα μία καλή αρχή, ωστόσο δεν αποτελεί εγγύηση. Για παράδειγμα, είναι το υψόμετρο και το γεωγραφικό πλάτος ένα καλό πρωτεύον κλειδί για το πλαίσιο airports;

airports |>
  count(alt, lat) |> 
  filter(n > 1)
#> # A tibble: 1 × 3
#>     alt   lat     n
#>   <dbl> <dbl> <int>
#> 1    13  40.6     2

Η αναγνώριση ενός αεροδρομίου με βάση το υψόμετρο και το γεωγραφικό του πλάτος είναι σαφώς κακή ιδέα και γενικά δεν είναι δυνατό να γνωρίζουμε μόνο από τα δεδομένα εάν ένας συνδυασμός μεταβλητών αποτελεί ένα καλό πρωτεύον κλειδί ή όχι. Ωστόσο, για τις πτήσεις, ο συνδυασμός των μεταβλητών time_hour, carrier, και flight φαίνεται λογικός γιατί θα προκαλούσε σύγχυση για μία αεροπορική εταιρεία και τους πελάτες της εάν υπήρχαν πολλές πτήσεις με τον ίδιο αριθμό πτήσης στον αέρα ταυτόχρονα .

Έχοντας ξεκαθαρίσει αυτό το σημείο, ίσως είναι καλύτερα να εισάγουμε ένα απλό αριθμητικό υποκατάστατο κλειδί χρησιμοποιώντας τον αριθμό κάθε γραμμής:

flights2 <- flights |> 
  mutate(id = row_number(), .before = 1)
flights2
#> # A tibble: 336,776 × 20
#>      id  year month   day dep_time sched_dep_time dep_delay arr_time
#>   <int> <int> <int> <int>    <int>          <int>     <dbl>    <int>
#> 1     1  2013     1     1      517            515         2      830
#> 2     2  2013     1     1      533            529         4      850
#> 3     3  2013     1     1      542            540         2      923
#> 4     4  2013     1     1      544            545        -1     1004
#> 5     5  2013     1     1      554            600        -6      812
#> 6     6  2013     1     1      554            558        -4      740
#> # ℹ 336,770 more rows
#> # ℹ 12 more variables: sched_arr_time <int>, arr_delay <dbl>, …

Τα υποκατάστατα κλειδιά μπορούν να είναι ιδιαίτερα χρήσιμα όταν επικοινωνείτε με άλλους ανθρώπους: είναι πολύ πιο εύκολο να πείτε σε κάποιον να ρίξει μία ματιά στην πτήση 2001 παρά να του πείτε να δει την UA430 που αναχώρησε στις 9 π.μ., στις 03-01-2013.

19.2.4 Ασκήσεις

Ξεχάσαμε να σχεδιάσουμε τη σχέση μεταξύ weather και airports στο Σχήμα 19.1. Ποια είναι η σχέση και πώς πρέπει να εμφανίζεται στο διάγραμμα;
Η μεταβλητή weather περιέχει μόνο πληροφορίες για τα τρία αεροδρόμια αναχώρησης στη Νέα Υόρκη. Εάν περιείχε αρχεία καιρού για όλα τα αεροδρόμια των ΗΠΑ, ποια πρόσθετη σύνδεση θα έκανε με το πλαίσιο δεδομένων flights;
Οι μεταβλητές year, month, day, hour, και origin σχεδόν σχηματίζουν ένα σύνθετο κλειδί για το πλαίσιο δεδομένων weather, ωστόσο υπάρχει μία τιμή ώρας που έχει διπλότυπες παρατηρήσεις. Μπορείτε να καταλάβετε τι το ιδιαίτερο έχει αυτή η ώρα;
Γνωρίζουμε ότι κάποιες μέρες του χρόνου είναι ιδιαίτερες και λιγότεροι άνθρωποι από το συνηθισμένο επιλέγουν να πετάξουν αυτές τις μέρες (για παράδειγμα, παραμονή και ανήμερα Χριστουγέννων). Πώς μπορείτε να αναπαραστήσετε αυτά τα δεδομένα ως πλαίσιο δεδομένων; Ποιο θα ήταν το πρωτεύον κλειδί; Πώς θα συνδεόταν με τα υπάρχοντα πλαίσια δεδομένων;
Σχεδιάστε ένα διάγραμμα που απεικονίζει τις συνδέσεις μεταξύ των πλαισίων δεδομένων Batting, People, και Salariesστο πακέτο Lahman. Σχεδιάστε ένα άλλο διάγραμμα που δείχνει τη σχέση μεταξύ των People, Managers, AwardsManagers. Πώς θα χαρακτηρίζατε τη σχέση μεταξύ των πλαισίων δεδομένων Batting, Pitching, και Fielding;

19.3 Βασικές ενώσεις

Τώρα που καταλαβαίνετε πως συνδέονται τα πλαίσια δεδομένων με τη βοήθεια κλειδιών, μπορούμε να αρχίσουμε να χρησιμοποιούμε ενώσεις για να κατανοήσουμε καλύτερα το σύνολο δεδομένων flights. Η dplyr προσφέρει έξι συναρτήσεις ένωσης: left_join(), inner_join(), right_join(), full_join(), semi_join(), και anti_join(). Όλες έχουν την ίδια διεπαφή: παίρνουν ένα ζευγάρι πλαισίων δεδομένων (x και y) και επιστρέφουν ένα πλαίσιο δεδομένων. Η σειρά των γραμμών και στηλών στην έξοδο καθορίζεται κυρίως από το x.

Σε αυτήν την ενότητα, θα μάθετε πώς να χρησιμοποιείτε μία ένωση αλλαγής, την left_join(), και δύο filtering ενώσεις, τις semi_join() και anti_join(). Στην επόμενη ενότητα, θα μάθετε πώς ακριβώς λειτουργούν αυτές οι συναρτήσεις, καθώς και για τις υπόλοιπες: inner_join(), right_join() και full_join().

19.3.1 Ενώσεις αλλαγής

Μία ένωση αλλαγής σας επιτρέπει να συνδυάσετε μεταβλητές από δύο πλαίσια δεδομένων: πρώτα αντιστοιχίζει παρατηρήσεις με βάση τα κλειδιά τους και μετά αντιγράφει παρατηρήσεις μεταξύ των μεταβλητών από το ένα πλαίσιο δεδομένων στο άλλο. Όπως και η mutate(), οι συναρτήσεις ένωσης προσθέτουν μεταβλητές στα δεξιά, οπότε αν το σύνολο δεδομένων σας έχει πολλές μεταβλητές, δεν θα δείτε τις νέες. Για αυτά τα παραδείγματα, θα διευκολύνουμε την παρατήρηση του τι συμβαίνει δημιουργώντας ένα πιο στενό σύνολο δεδομένων με έξι μόνο μεταβλητές¹:

flights2 <- flights |> 
  select(year, time_hour, origin, dest, tailnum, carrier)
flights2
#> # A tibble: 336,776 × 6
#>    year time_hour           origin dest  tailnum carrier
#>   <int> <dttm>              <chr>  <chr> <chr>   <chr>  
#> 1  2013 2013-01-01 05:00:00 EWR    IAH   N14228  UA     
#> 2  2013 2013-01-01 05:00:00 LGA    IAH   N24211  UA     
#> 3  2013 2013-01-01 05:00:00 JFK    MIA   N619AA  AA     
#> 4  2013 2013-01-01 05:00:00 JFK    BQN   N804JB  B6     
#> 5  2013 2013-01-01 06:00:00 LGA    ATL   N668DN  DL     
#> 6  2013 2013-01-01 05:00:00 EWR    ORD   N39463  UA     
#> # ℹ 336,770 more rows

Υπάρχουν τέσσερις τύποι ενώσεων αλλαγής, ωστόσο ένας είναι που θα χρησιμοποιείτε σχεδόν συνέχεια: left_join(). Αυτό είναι ιδιαίτερο γιατί η έξοδος θα έχει πάντα τις ίδιες γραμμές με το x, το πλαίσιο δεδομένων προς το οποίο συνδέετε². Η κύρια χρήση του left_join() είναι η προσθήκη επιπλέον μεταδεδομένων. Για παράδειγμα, μπορούμε να χρησιμοποιήσουμε το left_join() για να προσθέσουμε το πλήρες όνομα της αεροπορικής εταιρείας στα δεδομένα του flights2:

flights2 |>
  left_join(airlines)
#> Joining with `by = join_by(carrier)`
#> # A tibble: 336,776 × 7
#>    year time_hour           origin dest  tailnum carrier name                
#>   <int> <dttm>              <chr>  <chr> <chr>   <chr>   <chr>               
#> 1  2013 2013-01-01 05:00:00 EWR    IAH   N14228  UA      United Air Lines In…
#> 2  2013 2013-01-01 05:00:00 LGA    IAH   N24211  UA      United Air Lines In…
#> 3  2013 2013-01-01 05:00:00 JFK    MIA   N619AA  AA      American Airlines I…
#> 4  2013 2013-01-01 05:00:00 JFK    BQN   N804JB  B6      JetBlue Airways     
#> 5  2013 2013-01-01 06:00:00 LGA    ATL   N668DN  DL      Delta Air Lines Inc.
#> 6  2013 2013-01-01 05:00:00 EWR    ORD   N39463  UA      United Air Lines In…
#> # ℹ 336,770 more rows

Ή θα μπορούσαμε να μάθουμε τη θερμοκρασία και την ταχύτητα του ανέμου όταν κάθε αεροπλάνο αναχωρούσε:

flights2 |> 
  left_join(weather |> select(origin, time_hour, temp, wind_speed))
#> Joining with `by = join_by(time_hour, origin)`
#> # A tibble: 336,776 × 8
#>    year time_hour           origin dest  tailnum carrier  temp wind_speed
#>   <int> <dttm>              <chr>  <chr> <chr>   <chr>   <dbl>      <dbl>
#> 1  2013 2013-01-01 05:00:00 EWR    IAH   N14228  UA       39.0       12.7
#> 2  2013 2013-01-01 05:00:00 LGA    IAH   N24211  UA       39.9       15.0
#> 3  2013 2013-01-01 05:00:00 JFK    MIA   N619AA  AA       39.0       15.0
#> 4  2013 2013-01-01 05:00:00 JFK    BQN   N804JB  B6       39.0       15.0
#> 5  2013 2013-01-01 06:00:00 LGA    ATL   N668DN  DL       39.9       16.1
#> 6  2013 2013-01-01 05:00:00 EWR    ORD   N39463  UA       39.0       12.7
#> # ℹ 336,770 more rows

Ή τι μέγεθος αεροπλάνου πετούσε:

flights2 |> 
  left_join(planes |> select(tailnum, type, engines, seats))
#> Joining with `by = join_by(tailnum)`
#> # A tibble: 336,776 × 9
#>    year time_hour           origin dest  tailnum carrier type                
#>   <int> <dttm>              <chr>  <chr> <chr>   <chr>   <chr>               
#> 1  2013 2013-01-01 05:00:00 EWR    IAH   N14228  UA      Fixed wing multi en…
#> 2  2013 2013-01-01 05:00:00 LGA    IAH   N24211  UA      Fixed wing multi en…
#> 3  2013 2013-01-01 05:00:00 JFK    MIA   N619AA  AA      Fixed wing multi en…
#> 4  2013 2013-01-01 05:00:00 JFK    BQN   N804JB  B6      Fixed wing multi en…
#> 5  2013 2013-01-01 06:00:00 LGA    ATL   N668DN  DL      Fixed wing multi en…
#> 6  2013 2013-01-01 05:00:00 EWR    ORD   N39463  UA      Fixed wing multi en…
#> # ℹ 336,770 more rows
#> # ℹ 2 more variables: engines <int>, seats <int>

Όταν η left_join() δεν βρει ταίριασμα για μία γραμμή στο x, συμπληρώνει τις νέες μεταβλητές με κενές τιμές. Για παράδειγμα, δεν υπάρχουν πληροφορίες σχετικά με το αεροπλάνο με αναγνωριστικό κωδικό N3ALAA, οπότε οι τιμές στις στήλες type, engines, και seats θα λείπουν:

flights2 |> 
  filter(tailnum == "N3ALAA") |> 
  left_join(planes |> select(tailnum, type, engines, seats))
#> Joining with `by = join_by(tailnum)`
#> # A tibble: 63 × 9
#>    year time_hour           origin dest  tailnum carrier type  engines seats
#>   <int> <dttm>              <chr>  <chr> <chr>   <chr>   <chr>   <int> <int>
#> 1  2013 2013-01-01 06:00:00 LGA    ORD   N3ALAA  AA      <NA>       NA    NA
#> 2  2013 2013-01-02 18:00:00 LGA    ORD   N3ALAA  AA      <NA>       NA    NA
#> 3  2013 2013-01-03 06:00:00 LGA    ORD   N3ALAA  AA      <NA>       NA    NA
#> 4  2013 2013-01-07 19:00:00 LGA    ORD   N3ALAA  AA      <NA>       NA    NA
#> 5  2013 2013-01-08 17:00:00 JFK    ORD   N3ALAA  AA      <NA>       NA    NA
#> 6  2013 2013-01-16 06:00:00 LGA    ORD   N3ALAA  AA      <NA>       NA    NA
#> # ℹ 57 more rows

Θα επανέλθουμε σε αυτό το πρόβλημα μερικές φορές στο υπόλοιπο αυτού του κεφαλαίου.

19.3.2 Καθορισμός κλειδιών ένωσης

Από προεπιλογή, η left_join() θα χρησιμοποιεί όλες τις μεταβλητές που εμφανίζονται και στα δύο πλαίσια δεδομένων ως κλειδί ένωση, τη λεγόμενη φυσική (natural) ένωση. Αυτός είναι ένα χρήσιμος κανόνας, αλλά δεν λειτουργεί πάντα. Για παράδειγμα, τι θα συμβεί αν προσπαθήσουμε να ενώσουμε το flights2 με το πλήρες σύνολο δεδομένων planes;

flights2 |> 
  left_join(planes)
#> Joining with `by = join_by(year, tailnum)`
#> # A tibble: 336,776 × 13
#>    year time_hour           origin dest  tailnum carrier type  manufacturer
#>   <int> <dttm>              <chr>  <chr> <chr>   <chr>   <chr> <chr>       
#> 1  2013 2013-01-01 05:00:00 EWR    IAH   N14228  UA      <NA>  <NA>        
#> 2  2013 2013-01-01 05:00:00 LGA    IAH   N24211  UA      <NA>  <NA>        
#> 3  2013 2013-01-01 05:00:00 JFK    MIA   N619AA  AA      <NA>  <NA>        
#> 4  2013 2013-01-01 05:00:00 JFK    BQN   N804JB  B6      <NA>  <NA>        
#> 5  2013 2013-01-01 06:00:00 LGA    ATL   N668DN  DL      <NA>  <NA>        
#> 6  2013 2013-01-01 05:00:00 EWR    ORD   N39463  UA      <NA>  <NA>        
#> # ℹ 336,770 more rows
#> # ℹ 5 more variables: model <chr>, engines <int>, seats <int>, …

Θα λάβουμε πολλές περιπτώσεις χωρίς αντιστοίχιση επειδή η ένωση μας προσπαθεί να χρησιμοποιήσει τις μεταβλητές tailnum και year ως σύνθετο κλειδί. Και τα δύο σύνολα, flights και planes, περιέχουν μία στήλη year, ωστόσο αυτή η στήλη έχει σημαίνει διαφορετικά πράγματα σε κάθε περίπτωση: η flights$year είναι το έτος που πραγματοποιήθηκε η πτήση και η planes$year είναι το έτος κατασκευής του αεροπλάνου. Θέλουμε να πραγματοποιήσουμε ένωση μόνο με βάση την tailnum, επομένως πρέπει να παρέχουμε μία ρητή προδιαγραφή με το join_by():

flights2 |> 
  left_join(planes, join_by(tailnum))
#> # A tibble: 336,776 × 14
#>   year.x time_hour           origin dest  tailnum carrier year.y
#>    <int> <dttm>              <chr>  <chr> <chr>   <chr>    <int>
#> 1   2013 2013-01-01 05:00:00 EWR    IAH   N14228  UA        1999
#> 2   2013 2013-01-01 05:00:00 LGA    IAH   N24211  UA        1998
#> 3   2013 2013-01-01 05:00:00 JFK    MIA   N619AA  AA        1990
#> 4   2013 2013-01-01 05:00:00 JFK    BQN   N804JB  B6        2012
#> 5   2013 2013-01-01 06:00:00 LGA    ATL   N668DN  DL        1991
#> 6   2013 2013-01-01 05:00:00 EWR    ORD   N39463  UA        2012
#> # ℹ 336,770 more rows
#> # ℹ 7 more variables: type <chr>, manufacturer <chr>, model <chr>, …

Σημειώστε ότι η προέλευση των μεταβλητών year αποσαφηνίζεται στην έξοδο με ένα επίθημα (year.x και year.y), το οποίο μας λέει εάν η μεταβλητή προήλθε από το όρισμα x ή y. Μπορείτε να παρακάμψετε τα προεπιλεγμένα επιθήματα με το όρισμα suffix.

Το join_by(tailnum) είναι η σύντομη εκδοχή του join_by(tailnum == tailnum). Είναι σημαντικό να γνωρίζετε αυτήν την πληρέστερη εκδοχή για δύο λόγους. Πρώτον, γιατί περιγράφει τη σχέση μεταξύ των δύο πινάκων: τα κλειδιά πρέπει να είναι ίσα (equal). Αυτός είναι ο λόγος για τον οποίο αυτός ο τύπος ένωσης ονομάζεται συχνά equi ένωση. Θα μάθετε για τις non-equi ενώσεις στην Ενότητα 19.5.

Δεύτερον, γιατί δείχνει τον τρόπο με τον οποίο καθορίζετε διαφορετικά κλειδιά ένωσης σε κάθε πίνακα. Για παράδειγμα, υπάρχουν δύο τρόποι για να ενώσετε τους πίνακες flight2 και airports: είτε με βάση το dest (τον προορισμό) είτε το origin (την προέλευση):

flights2 |> 
  left_join(airports, join_by(dest == faa))
#> # A tibble: 336,776 × 13
#>    year time_hour           origin dest  tailnum carrier name                
#>   <int> <dttm>              <chr>  <chr> <chr>   <chr>   <chr>               
#> 1  2013 2013-01-01 05:00:00 EWR    IAH   N14228  UA      George Bush Interco…
#> 2  2013 2013-01-01 05:00:00 LGA    IAH   N24211  UA      George Bush Interco…
#> 3  2013 2013-01-01 05:00:00 JFK    MIA   N619AA  AA      Miami Intl          
#> 4  2013 2013-01-01 05:00:00 JFK    BQN   N804JB  B6      <NA>                
#> 5  2013 2013-01-01 06:00:00 LGA    ATL   N668DN  DL      Hartsfield Jackson …
#> 6  2013 2013-01-01 05:00:00 EWR    ORD   N39463  UA      Chicago Ohare Intl  
#> # ℹ 336,770 more rows
#> # ℹ 6 more variables: lat <dbl>, lon <dbl>, alt <dbl>, tz <dbl>, …

flights2 |> 
  left_join(airports, join_by(origin == faa))
#> # A tibble: 336,776 × 13
#>    year time_hour           origin dest  tailnum carrier name               
#>   <int> <dttm>              <chr>  <chr> <chr>   <chr>   <chr>              
#> 1  2013 2013-01-01 05:00:00 EWR    IAH   N14228  UA      Newark Liberty Intl
#> 2  2013 2013-01-01 05:00:00 LGA    IAH   N24211  UA      La Guardia         
#> 3  2013 2013-01-01 05:00:00 JFK    MIA   N619AA  AA      John F Kennedy Intl
#> 4  2013 2013-01-01 05:00:00 JFK    BQN   N804JB  B6      John F Kennedy Intl
#> 5  2013 2013-01-01 06:00:00 LGA    ATL   N668DN  DL      La Guardia         
#> 6  2013 2013-01-01 05:00:00 EWR    ORD   N39463  UA      Newark Liberty Intl
#> # ℹ 336,770 more rows
#> # ℹ 6 more variables: lat <dbl>, lon <dbl>, alt <dbl>, tz <dbl>, …

Σε παλαιότερο κώδικα, ενδέχεται να δείτε έναν διαφορετικό τρόπο καθορισμού των κλειδιών ένωσης, χρησιμοποιώντας ένα διάνυσμα χαρακτήρων:

Το by = "x" αντιστοιχεί στο join_by(x).
Το by = c("a" = "x") αντιστοιχεί στο join_by(a == x).

Ωστόσο, προτιμούμε το join_by() που υπάρχει πλέον, αφού παρέχει ένα πιο ξεκάθαρο και πιο ευέλικτο τρόπο προσδιορισμού.

Οι inner_join(), right_join(), και full_join() έχουν την ίδια διεπαφή με τη left_join(). Η διαφορά εντοπίζετε στο ποιες γραμμές διατηρούν: η αριστερή ένωση (left_join()) διατηρεί όλες τις γραμμές από το x, η δεξιά ένωση (right_join()) διατηρεί όλες τις γραμμές από το y, η πλήρης ένωση (full_join()) διατηρεί όλες τις γραμμές, είτε προέρχονται από το x είτε από το y και η εσωτερική ένωση (inner_join()) διατηρεί μόνο τις γραμμές που εμφανίζονται και στο x και στο y. Θα επανέλθουμε σε αυτά με περισσότερες λεπτομέρειες αργότερα.

19.3.3 Ενώσεις φιλτραρίσματος

Όπως μπορείτε να μαντέψετε, η κύρια ενέργεια μιας filtering ένωσης είναι το φιλτράρισμα των γραμμών Υπάρχουν δύο τύποι: ημι-ενώσεις και αντι-ενώσεις. Οι ημι-ενώσεις (semi-joins) διατηρούν όλες τις σειρές στο x που έχουν αντιστοιχία στο y. Για παράδειγμα, θα μπορούσαμε να χρησιμοποιήσουμε μία ημι-ένωση για να φιλτράρουμε το σύνολο δεδομένων airports για να διατηρήσουμε μόνο τα αεροδρόμια προέλευσης:

airports |> 
  semi_join(flights2, join_by(faa == origin))
#> # A tibble: 3 × 8
#>   faa   name                  lat   lon   alt    tz dst   tzone           
#>   <chr> <chr>               <dbl> <dbl> <dbl> <dbl> <chr> <chr>           
#> 1 EWR   Newark Liberty Intl  40.7 -74.2    18    -5 A     America/New_York
#> 2 JFK   John F Kennedy Intl  40.6 -73.8    13    -5 A     America/New_York
#> 3 LGA   La Guardia           40.8 -73.9    22    -5 A     America/New_York

Ή μόνο τους προορισμούς:

airports |> 
  semi_join(flights2, join_by(faa == dest))
#> # A tibble: 101 × 8
#>   faa   name                     lat    lon   alt    tz dst   tzone          
#>   <chr> <chr>                  <dbl>  <dbl> <dbl> <dbl> <chr> <chr>          
#> 1 ABQ   Albuquerque Internati…  35.0 -107.   5355    -7 A     America/Denver 
#> 2 ACK   Nantucket Mem           41.3  -70.1    48    -5 A     America/New_Yo…
#> 3 ALB   Albany Intl             42.7  -73.8   285    -5 A     America/New_Yo…
#> 4 ANC   Ted Stevens Anchorage…  61.2 -150.    152    -9 A     America/Anchor…
#> 5 ATL   Hartsfield Jackson At…  33.6  -84.4  1026    -5 A     America/New_Yo…
#> 6 AUS   Austin Bergstrom Intl   30.2  -97.7   542    -6 A     America/Chicago
#> # ℹ 95 more rows

Οι αντι-ενώσεις (anti-joins) είναι το αντίθετο: επιστρέφουν όλες τις γραμμές από το x που δεν έχουν αντιστοιχία στο y. Είναι χρήσιμα για την εύρεση κενών τιμών που είναι έμμεσες στα δεδομένα, το θέμα του Ενότητα 18.3. Οι τιμές που λείπουν σιωπηρά δεν εμφανίζονται ως NA αλλά υπάρχουν μόνο ως απουσία. Για παράδειγμα, μπορούμε να βρούμε γραμμές που λείπουν από το airports αναζητώντας πτήσεις που δεν έχουν αντίστοιχο αεροδρόμιο προορισμού:

flights2 |> 
  anti_join(airports, join_by(dest == faa)) |> 
  distinct(dest)
#> # A tibble: 4 × 1
#>   dest 
#>   <chr>
#> 1 BQN  
#> 2 SJU  
#> 3 STT  
#> 4 PSE

Ή μπορούμε να βρούμε ποιες τιμές της μεταβλητής tailnum λείπουν από το planes:

flights2 |>
  anti_join(planes, join_by(tailnum)) |> 
  distinct(tailnum)
#> # A tibble: 722 × 1
#>   tailnum
#>   <chr>  
#> 1 N3ALAA 
#> 2 N3DUAA 
#> 3 N542MQ 
#> 4 N730MQ 
#> 5 N9EAMQ 
#> 6 N532UA 
#> # ℹ 716 more rows

19.3.4 Ασκήσεις

Εντοπίστε τις 48 ώρες (κατά τη διάρκεια ολόκληρου του έτους) που έχουν τις χειρότερες καθυστερήσεις. Διασταυρώστε το με τα δεδομένα του weather. Μπορείτε να δείτε κάποιο μοτίβο;
Φανταστείτε ότι έχετε βρει τους 10 πιο δημοφιλείς προορισμούς χρησιμοποιώντας αυτόν τον κώδικα:
```
top_dest <- flights2 |>
  count(dest, sort = TRUE) |>
  head(10)
```
Πώς μπορείτε να βρείτε όλες τις πτήσεις προς αυτούς τους προορισμούς;
Έχει κάθε πτήση που αναχωρεί αντίστοιχα δεδομένα καιρού για εκείνη την ώρα;
Τι κοινό έχουν οι αναγνωριστικοί κωδικοί των αεροσκαφών που δεν έχουν αντίστοιχη εγγραφή στο planes; (Υπόδειξη: μία μεταβλητή εξηγεί ~90% των προβλημάτων.)
Προσθέστε μία στήλη στο planes που αναφέρει κάθε carrier που έχει χρησιμοποιήσει αυτό το αεροπλάνο. Μπορεί να περιμένετε ότι υπάρχει μία έμμεση σχέση μεταξύ αεροπλάνου και αεροπορικής εταιρείας, επειδή κάθε αεροπλάνο πετά με μία μόνο αεροπορική εταιρεία. Επιβεβαιώστε ή απορρίψτε αυτήν την υπόθεση χρησιμοποιώντας τα εργαλεία που έχετε μάθει σε προηγούμενα κεφάλαια.
Προσθέστε το γεωγραφικό πλάτος και μήκος του αεροδρομίου προέλευσης και προορισμού στο πλαίσιο δεδομένων flights. Είναι πιο εύκολο να μετονομάσετε τις στήλες πριν ή αφού κάνετε την ένωση;
Υπολογίστε τη μέση καθυστέρηση ανά προορισμό και, στη συνέχεια, ενώστε την πληροφορία στο airports, ώστε να μπορέσετε να παρουσιάσετε την κατανομή των καθυστερήσεων γεωγραφικά. Ακολουθεί ένας εύκολος τρόπος για να σχεδιάσετε έναν χάρτη των Ηνωμένων Πολιτειών:
```
airports |>
  semi_join(flights, join_by(faa == dest)) |>
  ggplot(aes(x = lon, y = lat)) +
    borders("state") +
    geom_point() +
    coord_quickmap()
```
Μπορεί να θέλετε να χρησιμοποιήσετε το size ή το color των σημείων για να εμφανίσετε τη μέση καθυστέρηση για κάθε αεροδρόμιο.
Τι συνέβη στις 13 Ιουνίου 2013; Σχεδιάστε έναν χάρτη με τις καθυστερήσεις και, στη συνέχεια, χρησιμοποιήστε το Google για να διασταυρώσετε τα δεδομένα για τον καιρό.

19.4 Πώς λειτουργούν οι ενώσεις;

Τώρα που έχετε χρησιμοποιήσει ενώσεις κάποιες φορές, ήρθε η ώρα να μάθετε περισσότερα σχετικά με τον τρόπο λειτουργίας τους, εστιάζοντας στο πώς κάθε γραμμή στο x αντιστοιχίζεται με τις γραμμές στο y. Θα ξεκινήσουμε εισάγοντας μία οπτική αναπαράσταση των ενώσεων, χρησιμοποιώντας τα απλά tibbles που ορίζονται παρακάτω και εμφανίζονται στο Σχήμα 19.2. Σε αυτά τα παραδείγματα θα χρησιμοποιήσουμε ένα μόνο κλειδί που ονομάζεται key και μία στήλη με μία τιμή (val_x και val_y), αλλά όλες οι ιδέες που χρησιμοποιούνται εδώ γενικεύονται σε πολλά κλειδιά και πολλαπλές τιμές.

x <- tribble(
  ~key, ~val_x,
     1, "x1",
     2, "x2",
     3, "x3"
)
y <- tribble(
  ~key, ~val_y,
     1, "y1",
     2, "y2",
     4, "y3"
)

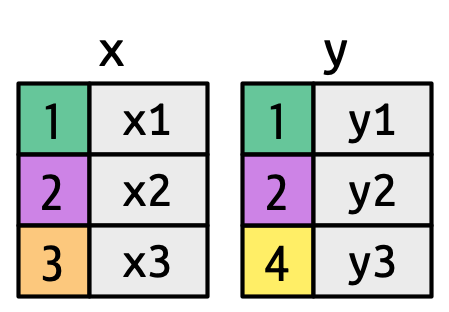
Τα x και y είναι δύο πλαίσια δεδομένων με 2 στήλες και 3 γραμμές, με περιεχόμενα όπως περιγράφοτναι στο κείμενο. Οι τιμές των κλειδιών είναι χρωματισμένες: το 1 αντιστοιχεί στο πράσινο, το 2 στο μωβ, το 3 στο πορτοκαλί και το 4 στο κίτρινο. — Σχήμα 19.2: Γραφική αναπαράσταση των δύο απλών πινάκων. Οι χρωματισμένες στήλες `key` αντιστοιχίζουν το χρώμα υποβάθρου στην τιμή του κλειδιού. Οι γκρι στήλες αντιπροσωπεύουν τις στήλες τιμών που μεταφέρονται στην πορεία.

Το Σχήμα 19.3 εισάγει τη βάση για την οπτική μας αναπαράσταση. Εμφανίζει όλες τις πιθανές αντιστοιχίσεις μεταξύ των x και y ως τομή μεταξύ των γραμμών που σχεδιάζονται από κάθε γραμμή του x και κάθε γραμμής του y. Οι γραμμές και οι στήλες στην έξοδο καθορίζονται κυρίως από το x, επομένως ο πίνακας x είναι οριζόντιος και ευθυγραμμίζεται με την έξοδο.

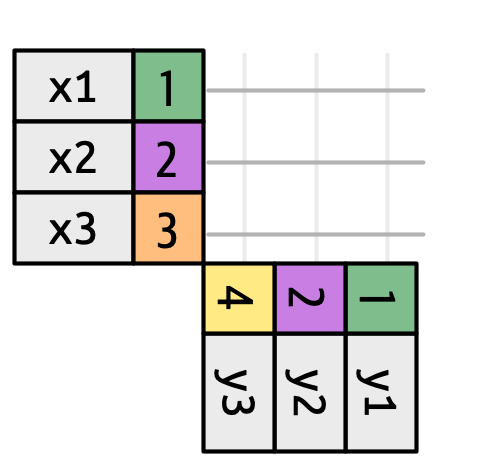
Τα x και y σχηματίζουν ορθή γωνία, με οριζόντιες γραμμές να εκτείνονται από το x και κάθετες γραμμές να εκτείνονται από το y. Υπάρχουν 3 γραμμές στο x και 3 γραμμές στο y, που έχει σαν αποτέλεσμα 9 τομές, που αντιπροσωπεύουν 9 πιθανούς συνδυασμούς. — Σχήμα 19.3: Για να κατανοήσετε πως δουλεύουν οι ενώσεις, είναι χρήσιμο να σκεφτείτε κάθε πιθανό συνδυασμό. Εδώ το δείχνουμε αυτό με ένα πλέγμα συνδεόμενων γραμμών.

Για να περιγράψουμε έναν συγκεκριμένο τύπο ένωσης, υποδεικνύουμε τις αντιστοιχίσεις με τελείες. Οι αντιστοιχίσεις καθορίζουν τις γραμμές στην έξοδο, ένα νέο πλαίσιο δεδομένων που περιέχει το κλειδί, τις τιμές x και τις τιμές y. Για παράδειγμα, το Σχήμα 19.4 δείχνει μία εσωτερική ένωση, όπου οι γραμμές διατηρούνται εάν και μόνο εάν τα κλειδιά είναι ίσα.

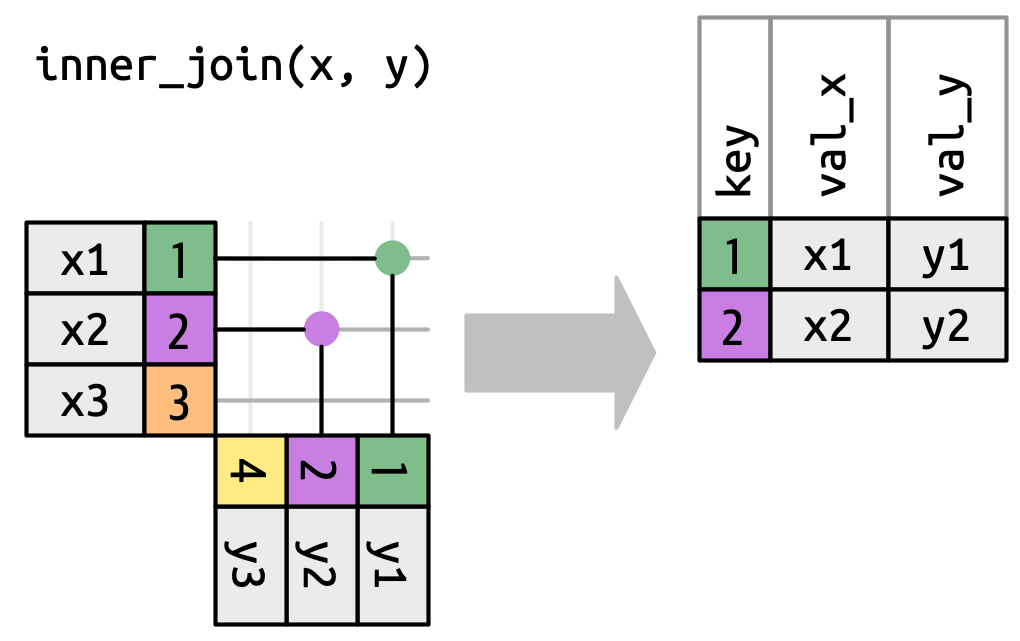
Τα x και y σχηματίζουν ορθή γωνία με γραμμές που σχηματίζουν ένα πλέγμα πιθανών συνδυασμών. Τα κλειδιά 1 και 2 εμφανίζονται τόσο στο x όσο και στο y, οπότε παίρνουμε έναν συνδυασμό που υποδεικνεύται από μία κουκίδα. Κάθε κουκίδα αντιστοιχεί σε μια γραμμή της εξόδου, οπότε το πλαίσιο δεδομένων που προκύπτει μετά την ένωση έχει δύο γραμμές. — Σχήμα 19.4: Μία εσωτερική ένωση αντιστοιχίζει κάθε γραμμή του `x` στη γραμμή του `y` που έχει την ίδια τιμή στο `key`. Κάθε συνδυασμός γίνεται μια γραμμή στην έξοδο.

Μπορούμε να εφαρμόσουμε τις ίδιες αρχές για να εξηγήσουμε τις εξωτερικές ενώσεις (outer joins), οι οποίες διατηρούν τις παρατηρήσεις που εμφανίζονται σε τουλάχιστον ένα από τα πλαίσια δεδομένων. Αυτές οι ενώσεις λειτουργούν προσθέτοντας μία πρόσθετη “εικονική” παρατήρηση σε κάθε πλαίσιο δεδομένων. Αυτή η παρατήρηση έχει ένα κλειδί που ταιριάζει αν δεν ταιριάζει άλλο κλειδί, και τιμές γεμάτες με NA. Υπάρχουν τρεις τύποι εξωτερικών ενώσεων:

Μία αριστερή ένωση (left join) διατηρεί όλες τις παρατηρήσεις του x, Σχήμα 19.5. Κάθε γραμμή του x διατηρείται στην έξοδο, μιας και μπορεί να αντιστοιχιστεί σε μία γραμμή με NA του y.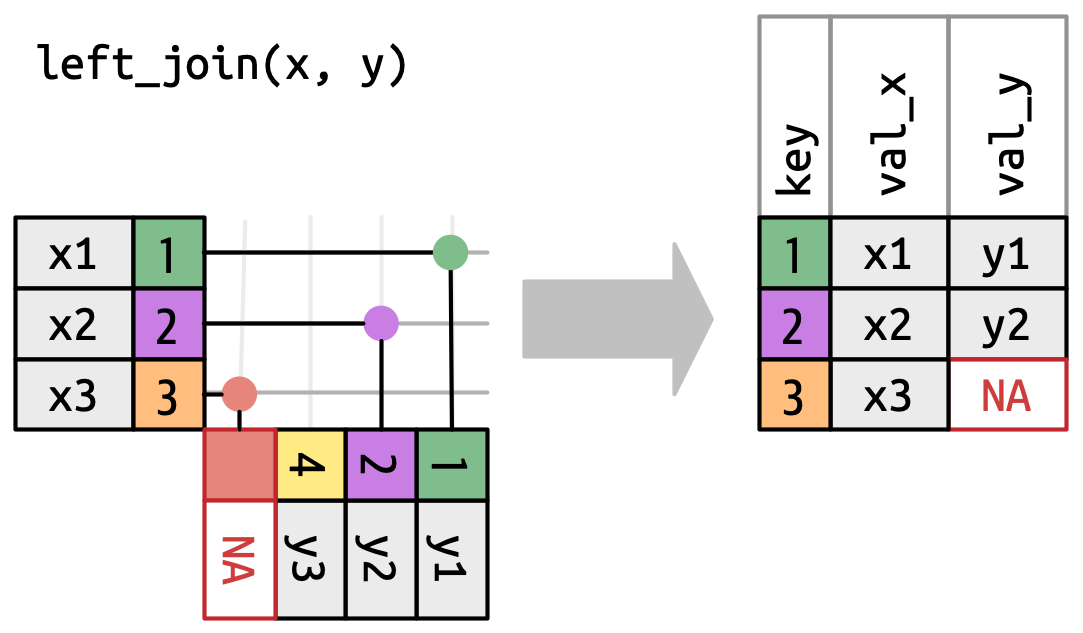

Σχήμα 19.5: Μία οπτική αναπαράσταση της αριστερής ένωσης όπου κάθε γραμμή του x εμφανίζεται στην έξοδο.
Μία δεξιά ένωση (right join) διατηρεί όλες τις παρατηρήσεις του y, Σχήμα 19.6. Κάθε γραμμή του y διατηρείται στην έξοδο, επειδή μπορεί να αντιστοιχιστεί σε μία γραμμή με NA του x. Η έξοδος εξακολουθεί να ταιριάζει με το x όσο το δυνατόν περισσότερο, ενώ τυχόν επιπλέον σειρές από το y προστίθενται στο τέλος.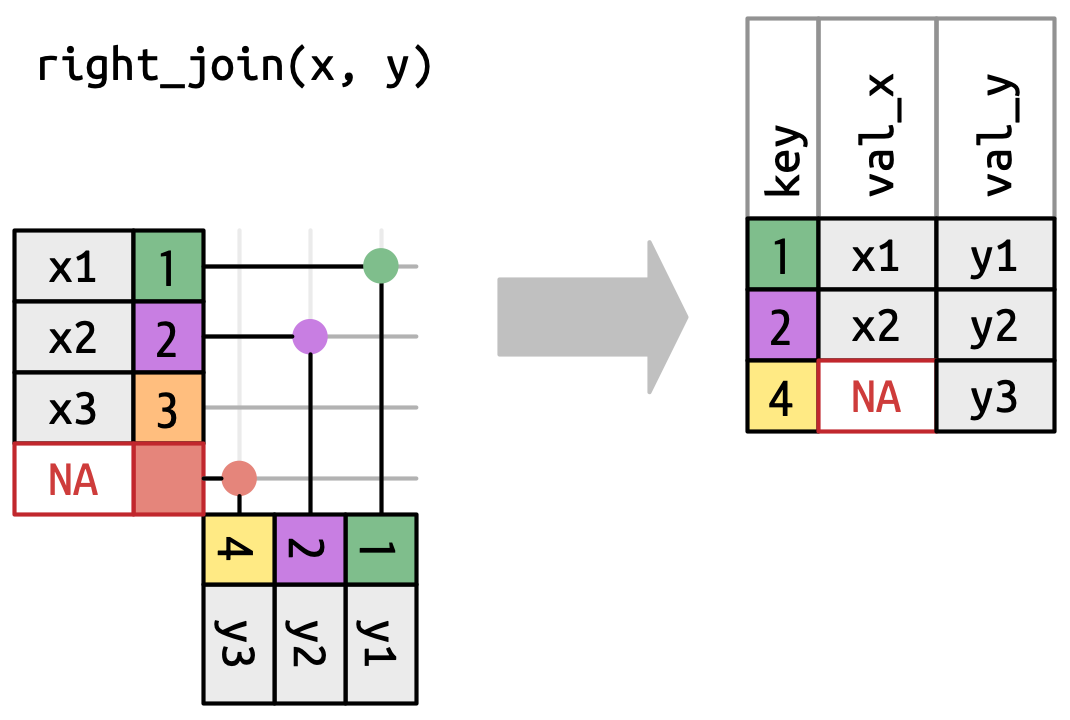

Σχήμα 19.6: Μία οπτική αναπαράσταση της δεξιάς ένωσης όπου κάθε γραμμή του y εμφανίζεται στην έξοδο.
Μία πλήρης ένωση (full join) διατηρεί όλες τις παρατηρήσεις που εμφανίζονται είτε στο x είτε στο y, Σχήμα 19.7. Κάθε γραμμή των x και y περιλαμβάνεται στην έξοδο επειδή και τα x και y περιλαμβάνουν μία εναλλακτική γραμμή με NA. Και πάλι, η έξοδος ξεκινά με όλες τις γραμμές από το x, ακολουθούμενες από τις υπόλοιπες γραμμές του y που δεν αντιστοιχίστηκαν σε συγκεκριμένη γραμμή του x.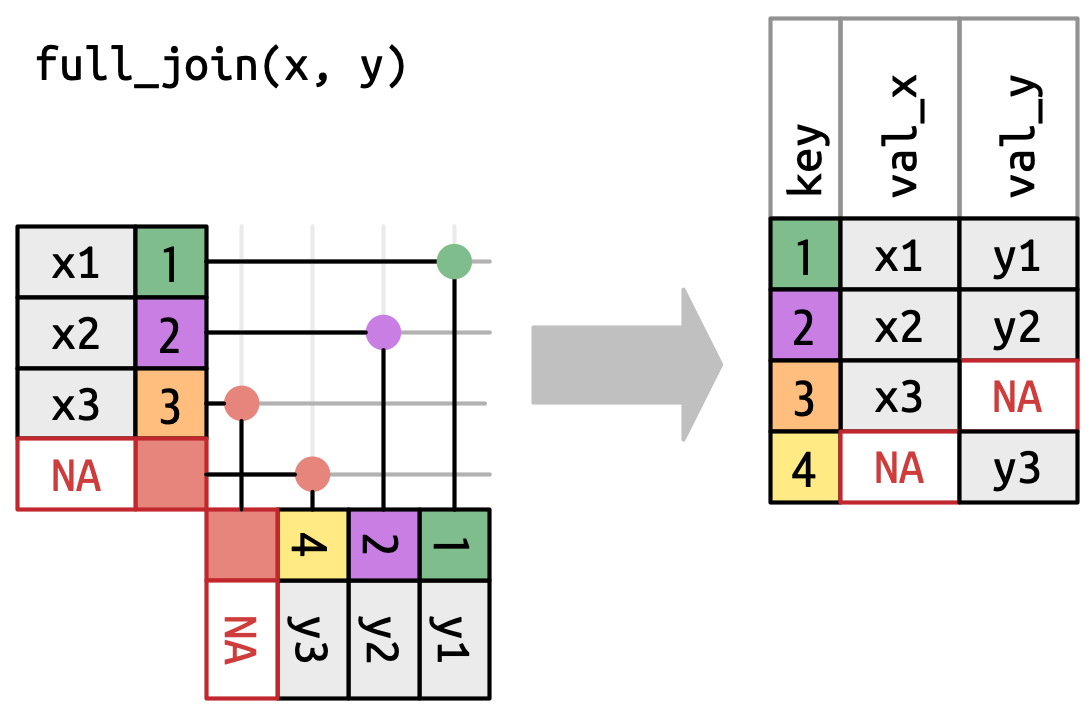

Σχήμα 19.7: Μία οπτική αναπαράσταση της πλήρους ένωσης όπου κάθε γραμμή τουx και του y εμφανίζεται στην έξοδο.

Ένας άλλος τρόπος για να δείξετε τις διαφορές ανάμεσα στους διάφορους τύπους της εξωτερικής ένωσης είναι με ένα διάγραμμα Venn, όπως στο Σχήμα 19.8. Ωστόσο, αυτή δεν είναι μία καλή αναπαράσταση, επειδή, ενώ μπορεί να φρεσκάρει τη μνήμη σας σχετικά με το ποιες γραμμές διατηρούνται, αποτυγχάνει όμως να επεξηγήσει τι συμβαίνει με τις στήλες.

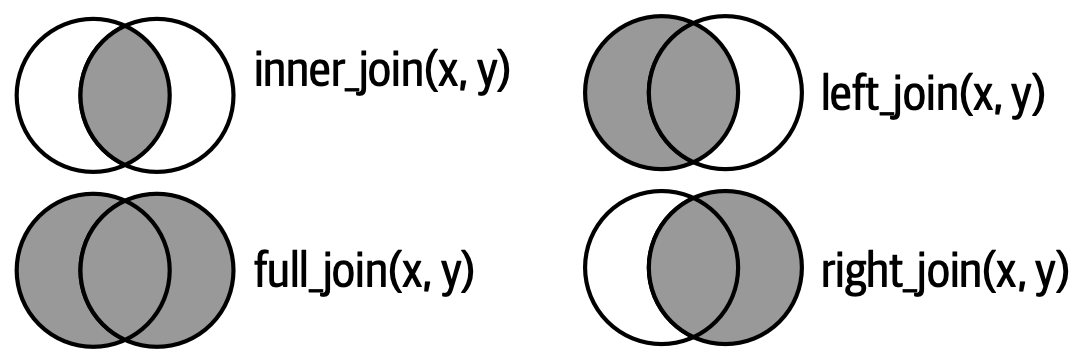
Διαγράμματα Venn για εσωτερικές, πλήρεις, αριστερές και δεξιές ενώσεις. Κάθε ένωση αναπαριστάται με δύο κύκλους που τέμνονται και αντιστοιχούν στα πλαίσια δεδομένανω x και y, με το x στα δεξιά και το y στα αριστερά. Η σκίαση υποδεικνύει το αποτέλεσμα της ένωσης. — Σχήμα 19.8: Διαγάμματα Venn που δείχνουν τη διαφορά ανάμεσα σε εσωτερικές, αριστερές, δεξιές και πλήρεις ενώσεις.

Οι ενώσεις που φαίνονται εδώ είναι οι λεγόμενες equi ενωσεις (ενώσεις ισοτιμίας), όπου οι γραμμές αντιστοιχίζονται εάν τα κλειδιά είναι ίσα. Οι ενώσεις ισοτιμίας είναι ο πιο συνηθισμένος τύπος ένωσης, επομένως συνήθως παραλείπουμε το πρόθεμα equi και απλώς λέμε “inner join” αντί για “equi inner join”. Θα επανέλθουμε στις non-equi ενώσεις στην Ενότητα 19.5.

19.4.1 Αντιστοίχιση γραμμών

Μέχρι στιγμής έχουμε εξερευνήσει τι συμβαίνει εάν μία γραμμή από το x ταιριάζει με μία ή καμμία γραμμή στο y. Τι συμβαίνει όμως αν ταιριάζει με περισσότερες από μία γραμμές; Για να κατανοήσουμε τι συμβαίνει, ας εστιάσουμε την προσοχή μας στο inner_join() και ας σχεδιάσουμε μία εικόνα, Σχήμα 19.9.

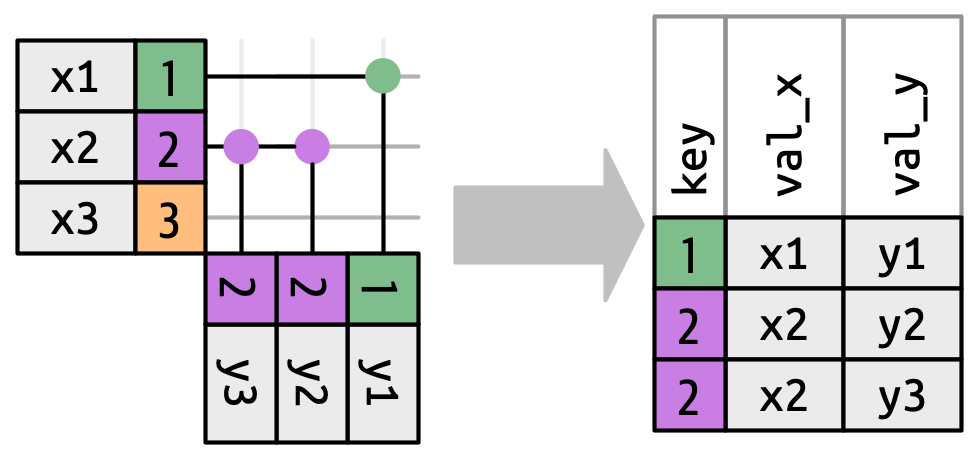
Ένα διάγραμμα ένωσης όπου το x έχει τιμές κλειδιών 1, 2 και 3, ενώ το y έχει τιμές κλειδιών 1, 2 και 2. Η έξοδος έχει τρεις γραμμές, επειδή το κλειδί 1 ταιριάζει με μία γραμμή, το κλειδί 2 ταιριάζει με 2 γραμμές και το κλειδί 3 δεν ταιριάζει με κάποια γραμμή. — Σχήμα 19.9: Οι τρεις τρόποι με τους οποίους μπορεί να αντιστοιχιστεί μια γραμμή στο `x`. Το `x1` αντιστοιχεί σε μία γραμμή στο `y`, το `x2` αντιστοιχεί σε δύο γραμμές στο `y`, το `x3` δεν αντιστοιχεί σε καμία γραμμή στο y. Σημειώστε ότι ενώ υπάρχουν τρεις γραμμές στο `x` και τρεις γραμμές στην έξοδο, δεν υπάρχει άμεση αντιστοιχία μεταξύ των γραμμών.

Υπάρχουν τρία πιθανά αποτελέσματα για μία γραμμή στο x:

Αν δεν ταιριάζει με τίποτα, απορρίπτεται.
Εάν ταιριάζει με 1 γραμμή στο y, διατηρείται.
Εάν αντιστοιχεί σε περισσότερες από 1 γραμμές στο y, γίνεται διπλότυπη μία φορά για κάθε αντιστοίχιση

Κατ’ αρχήν, αυτό σημαίνει ότι δεν υπάρχει εγγυημένη αντιστοιχία μεταξύ των γραμμών στην έξοδο και των γραμμών στο x, αλλά πρακτικά, αυτό σπάνια προκαλεί προβλήματα. Υπάρχει, ωστόσο, μία ιδιαίτερα επικίνδυνη περίπτωση που μπορεί να προκαλέσει μία συνδυαστική έκρηξη γραμμών. Φανταστείτε ότι ενώνετε τους παρακάτω δύο πίνακες:

df1 <- tibble(key = c(1, 2, 2), val_x = c("x1", "x2", "x3"))
df2 <- tibble(key = c(1, 2, 2), val_y = c("y1", "y2", "y3"))

Ενώ η πρώτη γραμμή του df1 αντιστοιχίζεται με μία μόνο γραμμή του df2, η δεύτερη και η τρίτη γραμμή αντιστοιχίζονται με από δύο γραμμές η καθεμία. Αυτό μπορεί να το συναντήσετε ως ένωση πολλά-με-πολλά, και θα έχει ως αποτέλεσμα το πακέτο dplyr να επιστρέψει μία προειδοποίηση:

df1 |> 
  inner_join(df2, join_by(key))
#> Warning in inner_join(df1, df2, join_by(key)): Detected an unexpected many-to-many relationship between `x` and `y`.
#> ℹ Row 2 of `x` matches multiple rows in `y`.
#> ℹ Row 2 of `y` matches multiple rows in `x`.
#> ℹ If a many-to-many relationship is expected, set `relationship =
#>   "many-to-many"` to silence this warning.
#> # A tibble: 5 × 3
#>     key val_x val_y
#>   <dbl> <chr> <chr>
#> 1     1 x1    y1   
#> 2     2 x2    y2   
#> 3     2 x2    y3   
#> 4     2 x3    y2   
#> 5     2 x3    y3

Εάν το κάνετε αυτό σκόπιμα, μπορείτε να ορίσετε relationship = "many-to-many",, όπως προτείνει η προειδοποίηση.

19.4.2 Ενώσεις φιλτραρίσματος

Ο αριθμός των αντιστοιχιών καθορίζει επίσης τη συμπεριφορά των ενώσεων φιλτραρίσματος. Η ημι-ένωση (semi-join) διατηρεί γραμμές στο x που έχουν μία ή περισσότερες αντιστοιχίσεις στο y, όπως στο Σχήμα 19.10. Η αντι-ένωση (anti-join) διατηρεί γραμμές στο x που δεν ταιριάζουν με καμία γραμμή στο y, όπως στο Σχήμα 19.11. Και στις δύο περιπτώσεις, μόνο η ύπαρξη μιας αντιστοίχισης είναι σημαντική, και όχι το πλήθος των αντιστοιχίσεων. Αυτό σημαίνει ότι οι ενώσεις φιλτραρίσματος δεν δημιουργούν ποτέ διπλότυπες γραμμές όπως κάνουν οι ενώσεις αλλαγής.

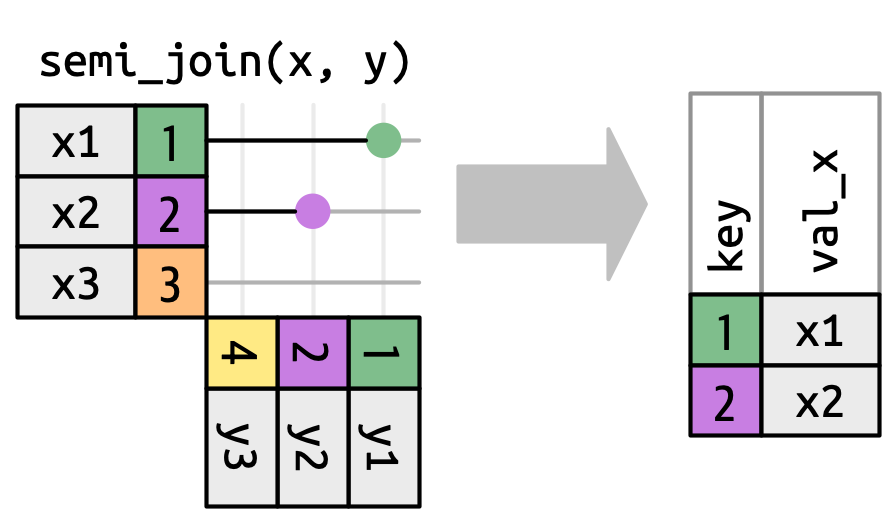
Ένα διάγραμμα ένωσης με τους παλιούς γνωστούς μας x και y. Σε μια ημι-ένωση, μόνο η παρουσία μιας αντιστοίχισης έχει σημασία, οπότε η έξοδος έχει τις ίδιες στήλες με το x. — Σχήμα 19.10: Σε μια ημι-ένωση το μόνο που έχει σημασία είναι να υπάρχει μια αντιστοίχιση, διαφορετικά οι τιμές στο πλαίσιο δεδομένων `y` δεν επηρεάζουν την έξοδο.

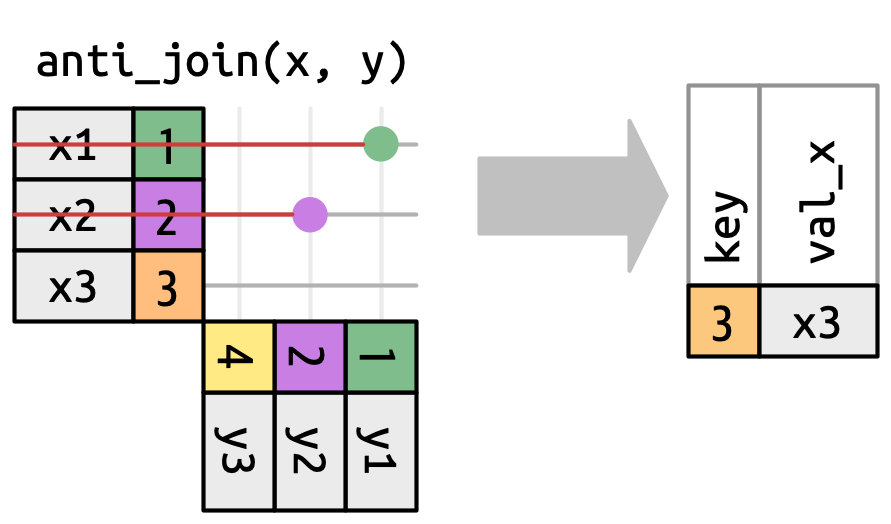
Μία αντι-ένωση είναι το αντίστροφο μιας ημι-ένωσης, οπότε οι αντιστοιχίσεις σχεδιάζονται με κόκκινες γραμμές, που υποδεικνύουν ότι αυτές οι γραμμές δεν θα εμφανιστούν στην έξοδο. — Σχήμα 19.11: Μία αντι-ένωση είναι το αντίστροφο μιας ημι-ένωσης, αφαιρώντας γραμμές από το `x` που αντιστοιχίζονται με το `y`.

19.5 Non-equi ενώσεις

Μέχρι στιγμής έχετε δει μόνο ενώσεις ισοτιμίας, ενώσεις όπου οι γραμμές ταιριάζουν εάν το κλειδί του x ισούται με το κλειδί στο y. Τώρα θα χαλαρώσουμε αυτόν τον περιορισμό και θα συζητήσουμε άλλους τρόπους για να προσδιορίσουμε εάν ένα ζευγάρι γραμμών ταιριάζει.

Αλλά προτού μπορέσουμε να το κάνουμε αυτό, πρέπει να επανεξετάσουμε μία απλοποίηση που κάναμε παραπάνω. Σε ισότιμες ενώσεις (equi joins) τα κλειδιά των x και y είναι πάντα ίσα, οπότε αρκεί να εμφανίσουμε μόνο ένα στην έξοδο. Μπορούμε να ζητήσουμε από το πακέτο dplyr να διατηρήσει και τα δύο κλειδιά με το όρισμα keep = TRUE, οδηγώντας στον παρακάτω κώδικα και στο επανασχεδιασμένο inner_join() στο Σχήμα 19.12.

x |> inner_join(y, join_by(key == key), keep = TRUE)
#> # A tibble: 2 × 4
#>   key.x val_x key.y val_y
#>   <dbl> <chr> <dbl> <chr>
#> 1     1 x1        1 y1   
#> 2     2 x2        2 y2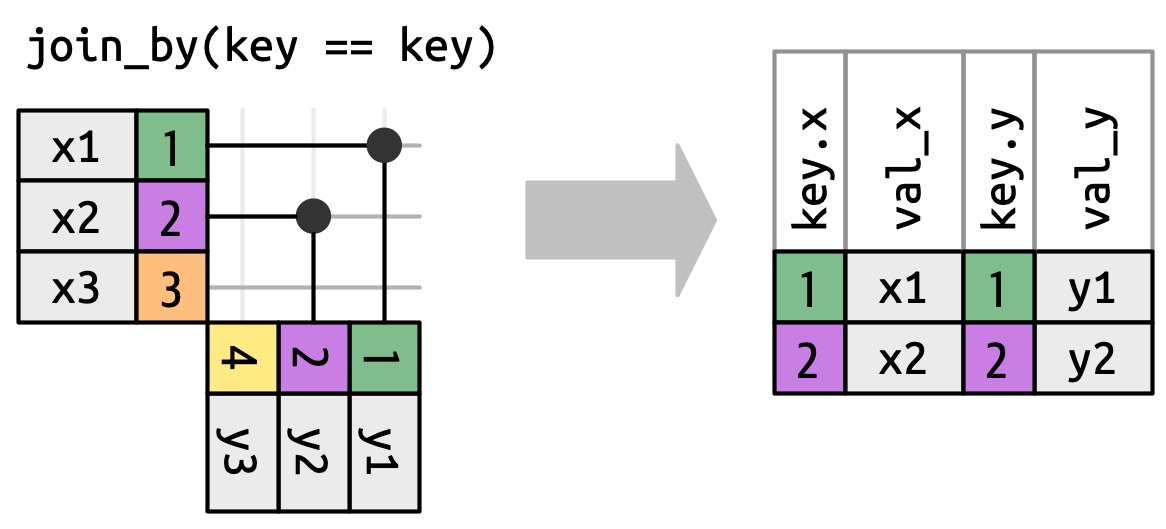

Ένα διάγραμμα ένωσης που δείχνει μια εσωτερική ένωση μεταξύ των x και y. Η έξοδος περιλαμβάνει πλέον τέσσερις στήλες: τις key.x, val_x, key.y και val_y. Οι τιμές των key.x και key.y είναι πανομοιότυπες, γι' αυτό συνήθως δείχνουμε μόνο μία από αυτές. — Σχήμα 19.12: Μία εσωτερική ένωση που δείνει τα κλειδιά των `x` και `y` στην έξοδο.

Όταν απομακρυνόμαστε από τις equi ενώσεις, θα εμφανίζουμε πάντα τα κλειδιά, επειδή οι τιμές των κλειδιών συχνά θα είναι διαφορετικές. Για παράδειγμα, αντί να κάνουμε την αντιστοίχιση μόνο όταν το x$key και το y$key είναι ίσα, θα μπορούσαμε να κάνουμε την αντιστοίχιση κάθε φορά που το x$key είναι μεγαλύτερο ή ίσο με το y$key, που οδηγεί στο Σχήμα 19.13. Οι συναρτήσεις ένωσης της dplyr κατανοούν αυτή τη διάκριση ανάμεσα σε ισοδύναμες και μη ισοδύναμες ενώσεις, επομένως θα εμφανίζουν πάντα και τα δύο κλειδιά όταν εκτελείτε μία ένωση χωρίς ισοδυναμία.

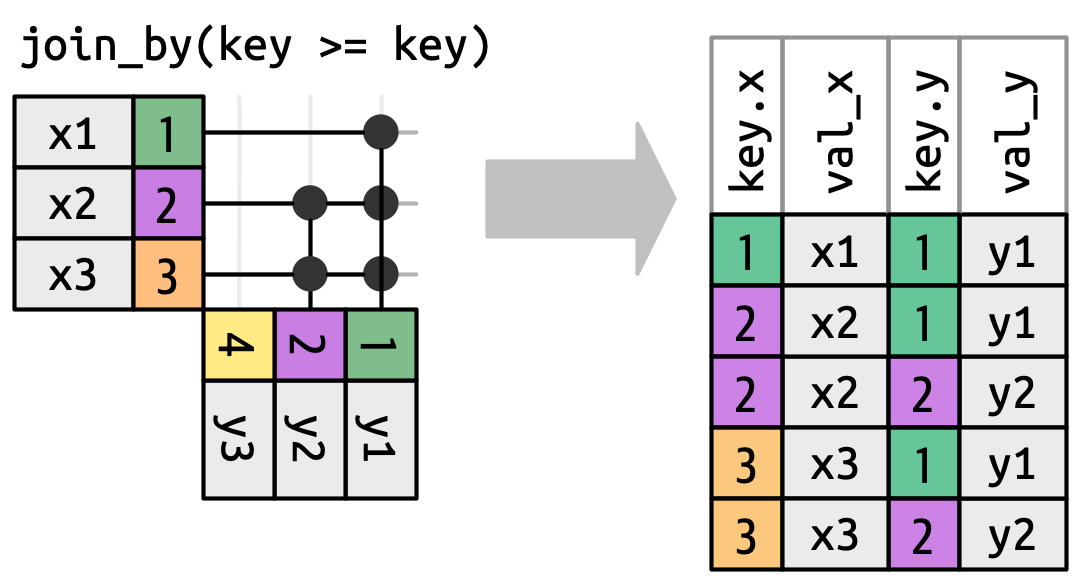
Ένα διάγραμμα ένωσης που απεικονίζει το αποτέλεσμα της join_by(key >= key). Η πρώτη γραμμή του x ταιριάζει με μία γραμμή του y, ενώ η δεύτερη και τρίτη γραμμή αντιστοιχίζονται με από δύο γραμμές η καθεμία. Αυτό σημαίνει ότι η έξοδος έχει πέντε γραμμές που περιέχουν κάθε ένα από τα ακόλουθα ζεύγη (key.x, key.y): (1, 1), (2, 1), (2, 2), (3, 1), (3, 2). — Σχήμα 19.13: Μία non-equi ένωση, όπου το κλειδί του `x` πρέπει να είναι μεγαλύτερο ή ίσο του κλειδιού του `y`. Πολλές γραμμές δημιουργούν πολλαπλές αντιστοιχίσεις.

Ο όρος “non-equi” ενώσεις δεν είναι ιδιαίτερα χρήσιμος, επειδή μας λέει μόνο τι δεν είναι η ένωση, όχι τι είναι. Η dplyr βοηθά προσδιορίζοντας τέσσερις ιδιαίτερα χρήσιμους τύπους non-equi join:

Οι διασταυρούμενες ενώσεις (Cross joins) αντιστοιχίζουν κάθε ζεύγος γραμμών
Οι ενώσεις ανισότητας (Inequality joins) χρησιμοποιούν τα <, <=, >, και >= αντί του ==.
Οι κυλιόμενες ενώσεις (Rolling joins) είναι παρόμοιες με τις ενώσεις ανισότητας αλλά βρίσκουν μόνο την πλησιέστερη αντιστοιχία.
Οι ενώσεις επικάλυψης (Overlap joins) είναι ένας ειδικός τύπος ένωσης ανισότητας που έχει σχεδιαστεί για να λειτουργεί με εύρη.

Κάθε μία από αυτές περιγράφεται λεπτομερέστερα στις επόμενες ενότητες.

19.5.1 Διασταυρούμενες ενώσεις

Μία διασταυρούμενη ένωση ταιριάζει με τα πάντα, όπως στο Σχήμα 19.14, δημιουργώντας το καρτεσιανό γινόμενο των γραμμών. Αυτό σημαίνει ότι η έξοδος θα έχει nrow(x) * nrow(y) γραμμές.

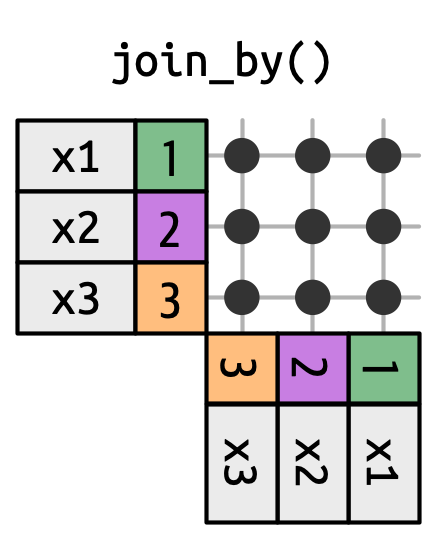
Ένα διάγραμμα ένωσης που δείνει μια κουκίδα για κάθε συνδυασμό των x και y. — Σχήμα 19.14: Μία διασταυρούμενη ένωησ αντιστοιχίζει κάθε γραμμή του `x` με κάθε γραμμή του `y`.

Οι διασταυρούμενες ενώσεις είναι χρήσιμες κατά τη δημιουργία συνδυασμών. Για παράδειγμα, ο παρακάτω κώδικας δημιουργεί κάθε πιθανό ζεύγος ονομάτων. Εφόσον ενώνουμε το df με τον εαυτό του, αυτό μερικές φορές ονομάζεται αυτο-ένωση (self-join). Οι διασταυρούμενες ενώσεις χρησιμοποιούν διαφορετική συνάρτηση ένωσης επειδή δεν υπάρχει διάκριση μεταξύ εσωτερικές/αριστερές/δεξιές/πλήρεις ενώσεις όταν η αντιστοίχιση αφορά κάθε γραμμή.

df <- tibble(name = c("John", "Simon", "Tracy", "Max"))
df |> cross_join(df)
#> # A tibble: 16 × 2
#>   name.x name.y
#>   <chr>  <chr> 
#> 1 John   John  
#> 2 John   Simon 
#> 3 John   Tracy 
#> 4 John   Max   
#> 5 Simon  John  
#> 6 Simon  Simon 
#> # ℹ 10 more rows

19.5.2 Ενώσεις ανισότητας

Οι ενώσεις ανισότητας χρησιμοποιούν τους τελεστές <, <=, >=, ή > για να περιορίσουν το σύνολο των πιθανών αντιστοιχίσεων, όπως στο Σχήμα 19.13 και το Σχήμα 19.15.

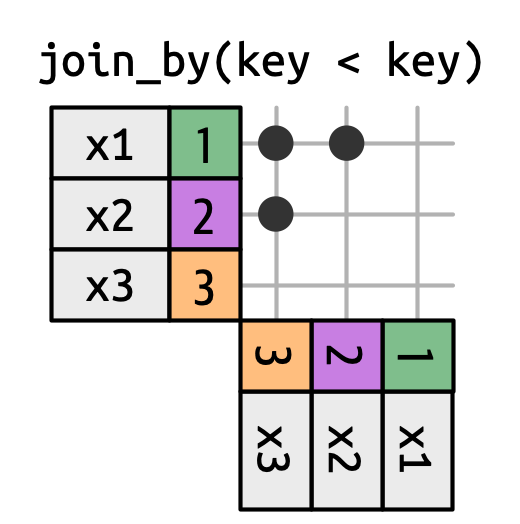
Ένα διάγραμμα που απεικονίζει μια ένωση ανισότητας όπου το πλαίδιο δεδομένων x ενώνεται με το πλαίσιο δεδομένων y όπου το κλειδί του x είναι μικρότερο από το κλειδί του y, δημιουργώντας έτσι ένα τριγωνικό σχήμα στην πάνω αριστερή γωνία. — Σχήμα 19.15: Μία ένωση ανισότητας όπου το `x` ενώνεται με το `y` στις γραμμές όπου το κλειδί του `x` είναι μικρότερο από το κλειδί του `y`. Αυτό δημιουργεί ένα τριγωνικό σχήμα στην πάρω αριστερή γωνία.

Οι ενώσεις ανισότητας είναι εξαιρετικά γενικές, τόσο γενικές που είναι δύσκολο να βρούμε ουσιαστικές συγκεκριμένες περιπτώσεις χρήσης. Μία μικρή χρήσιμη τεχνική είναι να τις χρησιμοποιούμε για να περιορίσουμε τη διασταυρούμενη ένωση έτσι ώστε αντί να δημιουργούμε όλες τις μεταθέσεις, να δημιουργούμε όλους τους συνδυασμούς:

df <- tibble(id = 1:4, name = c("John", "Simon", "Tracy", "Max"))

df |> inner_join(df, join_by(id < id))
#> # A tibble: 6 × 4
#>    id.x name.x  id.y name.y
#>   <int> <chr>  <int> <chr> 
#> 1     1 John       2 Simon 
#> 2     1 John       3 Tracy 
#> 3     1 John       4 Max   
#> 4     2 Simon      3 Tracy 
#> 5     2 Simon      4 Max   
#> 6     3 Tracy      4 Max

19.5.3 Κυλιόμενες ενώσεις

Οι κυλιόμενες ενώσεις είναι ένας ειδικός τύπος ένωσης ανισότητας όπου αντί να λαμβάνουμε κάθε γραμμή που ικανοποιεί την ανισότητα, παίρνουμε μόνο την πλησιέστερη γραμμή, όπως στο Σχήμα 19.16. Μπορείτε να μετατρέψετε οποιαδήποτε ένωση ανισότητας σε κυλιόμενη ένωση προσθέτοντας το όρισμα closest(). Για παράδειγμα, το join_by(closest(x <= y)) αντιστοιχεί στο μικρότερο y που είναι μεγαλύτερο ή ίσο με το x και το join_by(closest(x > y)) αντιστοιχεί στο μεγαλύτερο y που είναι μικρότερο από το x.

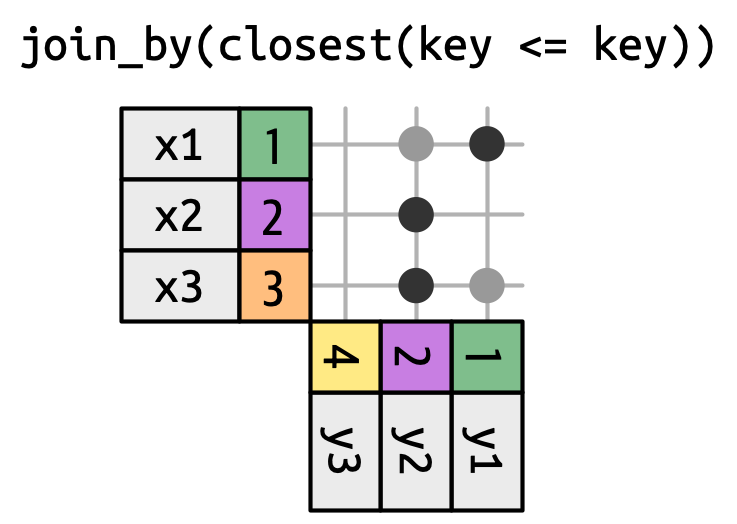
Μία κυλιώμενη ένωση είναι υποσύνολο μιας ένωσης ανισότητας, οπότε μερικές αντιστοιχίσεις είναι γκριζαρισμένες, υποδεικνύοντας ότι δεν χρησιμοποιούνται, μιας και δεν είναι οι "κοντινότερες". — Σχήμα 19.16: Μία κυλιώμενη ένωση είναι παρόμοια με μία μεγαλύτερο-από-ή-ίσο ένωση ανισότητας, αλλά αντιστοιχίζει μόνο την πρώτη τιμή.

Οι κυλιόμενες ενώσεις είναι ιδιαίτερα χρήσιμες όταν έχετε δύο πίνακες ημερομηνιών που δεν ευθυγραμμίζονται τέλεια και θέλετε να βρείτε (για παράδειγμα) την πλησιέστερη ημερομηνία στον πίνακα 1 που είναι πριν (ή μετά) κάποια ημερομηνία στον πίνακα 2.

Για παράδειγμα, φανταστείτε ότι είστε υπεύθυνος της επιτροπής σχεδιασμού εορτασμών για το γραφείο σας. Η εταιρεία σας θέλει να μην ξοδέψει πολλά χρήματα, επομένως αντί να κάνετε μεμονωμένα πάρτι, θα κάνετε ένα πάρτι μόνο, μία φορά το τρίμηνο. Οι κανόνες για τον καθορισμό του πότε θα γίνει ένα πάρτι είναι λίγο περίπλοκοι: τα πάρτι γίνονται πάντα Δευτέρα, παραλείπετε την πρώτη εβδομάδα του Ιανουαρίου, καθώς πολλοί είναι σε διακοπές, ενώ και η πρώτη Δευτέρα του τρίτου τριμήνου 2022 είναι στις 4 Ιουλίου, οπότε και σε αυτή την περίπτωση η ημερομηνία του πάρτι θα πρέπει να μεταφερθεί κατά μία εβδομάδα αργότερα. Αυτό οδηγεί στις ακόλουθες διαθέσιμες ημέρες για τα πάρτι:

parties <- tibble(
  q = 1:4,
  party = ymd(c("2022-01-10", "2022-04-04", "2022-07-11", "2022-10-03"))
)

Τώρα φανταστείτε ότι έχετε έναν πίνακα με τα γενέθλια των εργαζομένων:

set.seed(123)
employees <- tibble(
  name = sample(babynames::babynames$name, 100),
  birthday = ymd("2022-01-01") + (sample(365, 100, replace = TRUE) - 1)
)
employees
#> # A tibble: 100 × 2
#>   name     birthday  
#>   <chr>    <date>    
#> 1 Kemba    2022-01-22
#> 2 Orean    2022-06-26
#> 3 Kirstyn  2022-02-11
#> 4 Amparo   2022-11-11
#> 5 Belen    2022-03-25
#> 6 Rayshaun 2022-01-11
#> # ℹ 94 more rows

Και για κάθε εργαζόμενο θέλουμε να βρούμε τη πρώτη διαθέσιμη ημερομηνία για πάρτι που έρχεται μετά (ή πάνω στα) γενέθλιά του. Μπορούμε να το εκφράσουμε με μία κυλιόμενη ένωση:

employees |> 
  left_join(parties, join_by(closest(birthday >= party)))
#> # A tibble: 100 × 4
#>   name     birthday       q party     
#>   <chr>    <date>     <int> <date>    
#> 1 Kemba    2022-01-22     1 2022-01-10
#> 2 Orean    2022-06-26     2 2022-04-04
#> 3 Kirstyn  2022-02-11     1 2022-01-10
#> 4 Amparo   2022-11-11     4 2022-10-03
#> 5 Belen    2022-03-25     1 2022-01-10
#> 6 Rayshaun 2022-01-11     1 2022-01-10
#> # ℹ 94 more rows

Υπάρχει, ωστόσο, ένα πρόβλημα με αυτήν την προσέγγιση: οι άνθρωποι με γενέθλια πριν από τις 10 Ιανουαρίου δεν κάνουν πάρτι:

employees |> 
  anti_join(parties, join_by(closest(birthday >= party)))
#> # A tibble: 2 × 2
#>   name   birthday  
#>   <chr>  <date>    
#> 1 Maks   2022-01-07
#> 2 Nalani 2022-01-04

Για να το λύσουμε αυτό, θα χρειαστεί να αντιμετωπίσουμε το πρόβλημα με διαφορετικό τρόπο, χρησιμοποιώντας ενώσεις επικάλυψης.

19.5.4 Ενώσεις επικάλυψης

Οι ενώσεις επικάλυψης παρέχουν τρεις βοηθητικές συναρτήσεις που χρησιμοποιούν ενώσεις ανισότητας για να διευκολύνουν την εργασία με διαστήματα:

Η between(x, y_lower, y_upper) είναι η συντομογραφία του x >= y_lower, x <= y_upper.
Η within(x_lower, x_upper, y_lower, y_upper) είναι η συντομογραφία του x_lower >= y_lower, x_upper <= y_upper.
Η overlaps(x_lower, x_upper, y_lower, y_upper) είναι η συντομογραφία του x_lower <= y_upper, x_upper >= y_lower.

Ας συνεχίσουμε με το παράδειγμα γενεθλίων για να δούμε πώς μπορείτε να τα χρησιμοποιήσετε. Υπάρχει ένα πρόβλημα με τη στρατηγική που χρησιμοποιήσαμε παραπάνω: δεν υπάρχει πάρτι που να προηγείται των γενεθλίων που είναι μεταξύ 1-9 Ιανουαρίου. Επομένως, ίσως είναι καλύτερο να είμαστε σαφείς σχετικά με το εύρος ημερομηνιών που καλύπτει κάθε πάρτι και να κάνουμε μία ειδική περίπτωση για αυτά τα πρώιμα γενέθλια:

parties <- tibble(
  q = 1:4,
  party = ymd(c("2022-01-10", "2022-04-04", "2022-07-11", "2022-10-03")),
  start = ymd(c("2022-01-01", "2022-04-04", "2022-07-11", "2022-10-03")),
  end = ymd(c("2022-04-03", "2022-07-11", "2022-10-02", "2022-12-31"))
)
parties
#> # A tibble: 4 × 4
#>       q party      start      end       
#>   <int> <date>     <date>     <date>    
#> 1     1 2022-01-10 2022-01-01 2022-04-03
#> 2     2 2022-04-04 2022-04-04 2022-07-11
#> 3     3 2022-07-11 2022-07-11 2022-10-02
#> 4     4 2022-10-03 2022-10-03 2022-12-31

Ο Hadley είναι απελπιστικά κακός στην εισαγωγή δεδομένων, έτσι ήθελε επίσης να ελέγξει ότι οι περίοδοι που οργανώνονται τα πάρτι δεν αλληλεπικαλύπτονται. Ένας τρόπος για να το κάνετε αυτό είναι χρησιμοποιώντας μία αυτο-ένωση για να ελέγξετε εάν κάποιο διάστημα έναρξης-λήξης επικαλύπτεται με κάποιο άλλο:

parties |> 
  inner_join(parties, join_by(overlaps(start, end, start, end), q < q)) |> 
  select(start.x, end.x, start.y, end.y)
#> # A tibble: 1 × 4
#>   start.x    end.x      start.y    end.y     
#>   <date>     <date>     <date>     <date>    
#> 1 2022-04-04 2022-07-11 2022-07-11 2022-10-02

Υπάρχει μία επικάλυψη, οπότε ας διορθώσουμε αυτό το πρόβλημα και ας συνεχίσουμε:

parties <- tibble(
  q = 1:4,
  party = ymd(c("2022-01-10", "2022-04-04", "2022-07-11", "2022-10-03")),
  start = ymd(c("2022-01-01", "2022-04-04", "2022-07-11", "2022-10-03")),
  end = ymd(c("2022-04-03", "2022-07-10", "2022-10-02", "2022-12-31"))
)

Τώρα μπορούμε να ταιριάξουμε κάθε εργαζόμενο με το πάρτι του. Αυτό είναι ένα καλό παράδειγμα για να χρησιμοποιήσετε το όρισμα unmatched = "error", επειδή θέλουμε να μάθουμε γρήγορα εάν σε κάποιους υπαλλήλους δεν ανατέθηκε πάρτι.

employees |> 
  inner_join(parties, join_by(between(birthday, start, end)), unmatched = "error")
#> # A tibble: 100 × 6
#>   name     birthday       q party      start      end       
#>   <chr>    <date>     <int> <date>     <date>     <date>    
#> 1 Kemba    2022-01-22     1 2022-01-10 2022-01-01 2022-04-03
#> 2 Orean    2022-06-26     2 2022-04-04 2022-04-04 2022-07-10
#> 3 Kirstyn  2022-02-11     1 2022-01-10 2022-01-01 2022-04-03
#> 4 Amparo   2022-11-11     4 2022-10-03 2022-10-03 2022-12-31
#> 5 Belen    2022-03-25     1 2022-01-10 2022-01-01 2022-04-03
#> 6 Rayshaun 2022-01-11     1 2022-01-10 2022-01-01 2022-04-03
#> # ℹ 94 more rows

19.5.5 Ασκήσεις

Μπορείτε να εξηγήσετε τι συμβαίνει με τα κλειδιά σε αυτή την ένωση ισοδυναμίας; Γιατί είναι διαφορετικά;

x |> full_join(y, join_by(key == key))
#> # A tibble: 4 × 3
#>     key val_x val_y
#>   <dbl> <chr> <chr>
#> 1     1 x1    y1   
#> 2     2 x2    y2   
#> 3     3 x3    <NA> 
#> 4     4 <NA>  y3

x |> full_join(y, join_by(key == key), keep = TRUE)
#> # A tibble: 4 × 4
#>   key.x val_x key.y val_y
#>   <dbl> <chr> <dbl> <chr>
#> 1     1 x1        1 y1   
#> 2     2 x2        2 y2   
#> 3     3 x3       NA <NA> 
#> 4    NA <NA>      4 y3

Για να βρούμε εάν οι περίοδοι των πάρτι επικαλύπτονται με άλλα πάρτι χρησιμοποιήσαμε το q < q στην join_by(). Γιατί; Τι συμβαίνει εάν αφαιρέσουμε αυτή την ανισότητα;

19.6 Σύνοψη

Σε αυτό το κεφάλαιο, μάθατε πώς να χρησιμοποιείτε ενώσεις αλλαγής και ενώσεις φιλτραρίσματος για να συνδυάσετε δεδομένα από ένα ζεύγος πλαισίων δεδομένων. Στην πορεία μάθατε πώς να αναγνωρίζετε κλειδιά και τη διαφορά μεταξύ πρωτεύοντος και ξένου κλειδιού. Καταλαβαίνετε επίσης πώς λειτουργούν οι ενώσεις και πώς να υπολογίσετε πόσες γραμμές θα έχει η έξοδος. Τέλος, ρίξατε μία ματιά στη δύναμη των non-equi ενώσεων και έχετε δει μερικές ενδιαφέρουσες περιπτώσεις χρήσης.

Αυτό το κεφάλαιο ολοκληρώνει το μέρος “Μετασχηματισμός” αυτού του βιβλίου, όπου η το ενδιαφέρον μας ήταν στα εργαλεία που θα μπορούσατε να χρησιμοποιήσετε με μεμονωμένες στήλες και tibbles. Μάθατε για συναρτήσεις από το πακέτο dplyr και από το βασικό σύνολο συναρτήσεων της R για εργασία με λογικά διανύσματα, αριθμούς και πλήρεις πίνακες, τις συναρτήσεις του πακέτου stringr για εργασία με συμβολοσειρές, τις συναρτήσεις του πακέτου lubridate για εργασία με ημερομηνίες-ώρες και τις συναρτήσεις του forcats για εργασία με παράγοντες.

Στο επόμενο μέρος του βιβλίου, θα μάθετε περισσότερα σχετικά με τη μετατροπή διαφόρων τύπων δεδομένων στην R σε μία τακτοποιημένη (tidy) μορφή.

Να θυμάστε ότι στο RStudio μπορείτε επίσης να χρησιμοποιήσετε το View() για να αποφύγετε αυτό το πρόβλημα.↩︎
Αυτό δεν είναι 100% αλήθεια, αλλά θα λαμβάνετε μία προειδοποίηση όποτε δεν είναι.↩︎