13 Αριθμητικά διανύσματα

13.1 Εισαγωγή

Τα αριθμητικά διανύσματα είναι η ραχοκοκαλιά της επιστήμης των δεδομένων και τα έχετε ήδη χρησιμοποιήσει αρκετές φορές σε προηγούμενα κεφάλαια αυτού του βιβλίου. Είναι ώρα πλέον να εξερευνήσετε τι μπορείτε να κάνετε με αυτά στην R, διασφαλίζοντας ότι είστε κατάλληλα εξοπλισμένοι για να αντιμετωπίσετε οποιοδήποτε μελλοντικό πρόβλημα σχετικό με αριθμητικά διανύσματα.

Θα ξεκινήσουμε δίνοντάς σας μερικά εργαλεία για να δημιουργήσετε αριθμούς από συμβολοσειρές και θα προχωρήσουμε σε λίγες περισσότερες λεπτομέρειες για την count(). Στη συνέχεια, θα εμβαθύνουμε σε διάφορους αριθμητικούς μετασχηματισμούς που συνδυάζονται καλά με την mutate(), συμπεριλαμβανομένων και πιο γενικών μετασχηματισμών που μπορούν να εφαρμοστούν σε άλλους τύπους διανυσμάτων, αλλά χρησιμοποιούνται συχνά με αριθμητικά διανύσματα. Θα ολοκληρώσουμε καλύπτοντας τις συναρτήσεις σύνοψης που συνδυάζονται ωραία με την summarize() και θα σας δείξουμε πώς μπορούν ακόμα να χρησιμοποιηθούν με την mutate().

13.1.1 Προαπαιτούμενα

Αυτό το κεφάλαιο χρησιμοποιεί συναρτήσεις κυρίως από το βασικό πακέτο λειτουργιών της R, οι οποίες είναι διαθέσιμες χωρίς φόρτωση κάποιου πακέτου. Ωστόσο, χρειαζόμαστε ακόμα το tidyverse, γιατί θα χρησιμοποιήσουμε αυτές τις βασικές συναρτήσεις της R μέσα σε συναρτήσεις του tidyverse, όπως στην mutate() και την filter(). Όπως και στο προηγούμενο κεφάλαιο, έτσι και εδώ θα χρησιμοποιήσουμε πραγματικά παραδείγματα από το σύνολο δεδομένων nycflights13, καθώς και τυχαία παραδείγματα που δημιουργήθηκαν με την c() και την tribble().

library(tidyverse)
library(nycflights13)

13.2 Δημιουργώντας αριθμούς

Στις περισσότερες περιπτώσεις, θα έχετε αριθμούς που υπάρχουν ήδη ως ένας απο τους αριθμητικούς τύπους δεδομένων της R: ακέραιους (integer) ή κινητής υποδιαστολής (γνωστοί και ως διπλής ακρίβειας, double). Σε ορισμένες περιπτώσεις, ωστόσο, θα τους συναντήσετε ως συμβολοσειρές, πιθανώς επειδή τις έχετε δημιουργήσει μέσω ενός συγκεντρωτικού πίνακα ή επειδή κάτι πήγε στραβά κατά την εισαγωγή των δεδομένων σας.

Η readr παρέχει δύο χρήσιμες συναρτήσεις για την ανάλυση συμβολοσειρών σε αριθμούς: την parse_double() και την parse_number(). Χρησιμοποιήστε την parse_double() όταν έχετε αριθμούς που έχουν γραφτεί ως συμβολοσειρές:

x <- c("1.2", "5.6", "1e3")
parse_double(x)
#> [1]    1.2    5.6 1000.0

Χρησιμοποιήστε την parse_number() όταν η συμβολοσειρά περιέχει μη αριθμητικό κείμενο που θέλετε να αγνοήσετε. Είναι ιδιαίτερα χρήσιμη για δεδομένα συναλλάγματος και ποσοστά:

x <- c("$1,234", "USD 3,513", "59%")
parse_number(x)
#> [1] 1234 3513   59

13.3 Καταμετρήσεις

Είναι εκπληκτικό το πόση επιστήμη δεδομένων μπορείτε να εφαρμόσετε χρησιμοποιώντας μόνο μετρήσεις και λίγη βασική αριθμητική. Για αυτό, το πακέτο dplyr προσπαθεί να κάνει τη μέτρηση όσο το δυνατόν πιο εύκολη με την count(). Η συνάρτηση αυτή είναι εξαιρετική για γρήγορη εξερεύνηση και ελέγχους κατά την ανάλυση των δεδομένων:

flights |> count(dest)
#> # A tibble: 105 × 2
#>   dest      n
#>   <chr> <int>
#> 1 ABQ     254
#> 2 ACK     265
#> 3 ALB     439
#> 4 ANC       8
#> 5 ATL   17215
#> 6 AUS    2439
#> # ℹ 99 more rows

(Παρά τις συμβουλές της ενότητας Κεφάλαιο 4, συνήθως βάζουμε την count() σε μία ξεχωριστή γραμμή καθώς συχνά χρησιμοποιείται στην κονσόλα για να ελέγξουμε γρήγορα ότι ένας υπολογισμός λειτουργεί όπως αναμένεται.)

Εάν θέλετε να δείτε τις πιο συνηθισμένες τιμές, προσθέστε το όρισμα sort = TRUE:

flights |> count(dest, sort = TRUE)
#> # A tibble: 105 × 2
#>   dest      n
#>   <chr> <int>
#> 1 ORD   17283
#> 2 ATL   17215
#> 3 LAX   16174
#> 4 BOS   15508
#> 5 MCO   14082
#> 6 CLT   14064
#> # ℹ 99 more rows

Και να θυμάστε ότι εάν θέλετε να δείτε όλες τις τιμές, μπορείτε να χρησιμοποιήσετε το |> View() ή το |> print(n = Inf).

Μπορείτε να εκτελέσετε τον ίδιο υπολογισμό “με το χέρι” με τις group_by(), summarize() και n(). Αυτό είναι χρήσιμο επειδή σας επιτρέπει να υπολογίζετε και άλλες περιλήψεις ταυτόχρονα:

flights |> 
  group_by(dest) |> 
  summarize(
    n = n(),
    delay = mean(arr_delay, na.rm = TRUE)
  )
#> # A tibble: 105 × 3
#>   dest      n delay
#>   <chr> <int> <dbl>
#> 1 ABQ     254  4.38
#> 2 ACK     265  4.85
#> 3 ALB     439 14.4 
#> 4 ANC       8 -2.5 
#> 5 ATL   17215 11.3 
#> 6 AUS    2439  6.02
#> # ℹ 99 more rows

Η n() είναι μία ειδική συνάρτηση σύνοψης που δεν δέχεται ορίσματα και αντ’ αυτού έχει πρόσβαση σε πληροφορίες σχετικά με την “τρέχουσα” ομάδα. Αυτό σημαίνει ότι λειτουργεί μόνο μέσα σε συναρτήσεις της dplyr:

n()
#> Error in `n()`:
#> ! Must only be used inside data-masking verbs like `mutate()`,
#>   `filter()`, and `group_by()`.

Υπάρχουν μερικές παραλλαγές της n() και της count() που μπορεί να σας φανούν χρήσιμες:

Η n_distinct(x) μετρά τον αριθμό των διακριτών (μοναδικών) τιμών μιας ή περισσότερων μεταβλητών. Για παράδειγμα, θα μπορούσαμε να καταλάβουμε ποιοι προορισμοί εξυπηρετούνται από τις περισσότερες εταιρείες:
```
flights |> 
  group_by(dest) |> 
  summarize(carriers = n_distinct(carrier)) |> 
  arrange(desc(carriers))
#> # A tibble: 105 × 2
#>   dest  carriers
#>   <chr>    <int>
#> 1 ATL          7
#> 2 BOS          7
#> 3 CLT          7
#> 4 ORD          7
#> 5 TPA          7
#> 6 AUS          6
#> # ℹ 99 more rows
```
Μία σταθμισμένη καταμέτρηση είναι ένα άθροισμα. Για παράδειγμα, θα μπορούσατε να “μετρήσετε” τον αριθμό των μιλίων που πέταξε κάθε αεροπλάνο:
```
flights |> 
  group_by(tailnum) |> 
  summarize(miles = sum(distance))
#> # A tibble: 4,044 × 2
#>   tailnum  miles
#>   <chr>    <dbl>
#> 1 D942DN    3418
#> 2 N0EGMQ  250866
#> 3 N10156  115966
#> 4 N102UW   25722
#> 5 N103US   24619
#> 6 N104UW   25157
#> # ℹ 4,038 more rows
```
Οι σταθμισμένες καταμετρήσεις είναι ένα κοινό πρόβλημα, επομένως η count() έχει το όρισμα wt που λαμβάνει υπόψη ακριβώς αυτό:
```
flights |> count(tailnum, wt = distance)
```

Μπορείτε να μετρήσετε τις τιμές που λείπουν συνδυάζοντας την sum() και την is.na(). Στο σύνολο δεδομένων flights αυτό αντιπροσωπεύει πτήσεις που ακυρώνονται:

flights |> 
  group_by(dest) |> 
  summarize(n_cancelled = sum(is.na(dep_time))) 
#> # A tibble: 105 × 2
#>   dest  n_cancelled
#>   <chr>       <int>
#> 1 ABQ             0
#> 2 ACK             0
#> 3 ALB            20
#> 4 ANC             0
#> 5 ATL           317
#> 6 AUS            21
#> # ℹ 99 more rows

13.3.1 Ασκήσεις

Πώς μπορείτε να χρησιμοποιήσετε την count() για να καταμετρήσετε τις αριθμητικές γραμμές με μία κενή τιμή για μία μεταβλητή;
Αντικαταστήστε την count() στις παρακάτω κλήσεις της, χρησιμοποιώντας τις group_by(), summarize() και arrange():
1. flights |> count(dest, sort = TRUE)
2. flights |> count(tailnum, wt = distance)

13.4 Αριθμητικοί μετασχηματισμοί

Οι συναρτήσεις μετασχηματισμού λειτουργούν καλά με την mutate() επειδή η έξοδος τους είναι το ίδιο μήκος με την είσοδο. Η συντριπτική πλειοψηφία των συναρτήσεων μετασχηματισμού είναι ήδη ενσωματωμένες στο βασικό πακέτο λειτουργιών της R. Μιας και δεν θα ήταν πρακτικό να αναφερθούμε σε όλα, αυτή η ενότητα θα δείξει τα πιο χρήσιμα. Για παράδειγμα, ενώ η R παρέχει όλες τις τριγωνομετρικές συναρτήσεις που μπορεί να φανταστείτε, δεν τις αναφέρουμε εδώ επειδή σπάνια θα χρειαστούν στην επιστήμη των δεδομένων.

13.4.1 Κανόνες αριθμητικής και ανακύκλωσης

Είπαμε για τα βασικά της αριθμητικής (+, -, *, /, ^) στο Κεφάλαιο 2 και τα έχουμε χρησιμοποιήσει αρκετά από τότε. Οι συναρτήσεις αυτές δεν χρειάζονται εκτενείς εξηγήσεις, καθώς κάνουν ακριβώς ό,τι μάθατε στο δημοτικό. Πρέπει όμως να μιλήσουμε εν συντομία για τους κανόνες ανακύκλωσης που καθορίζουν τι συμβαίνει όταν η αριστερή και η δεξιά πλευρά έχουν διαφορετικά μήκη. Αυτό είναι σημαντικό για λειτουργίες όπως flights |> mutate(air_time = air_time / 60), επειδή υπάρχουν 336.776 αριθμοί στα αριστερά του / αλλά μόνο ένας στα δεξιά.

Η R χειρίζεται άνισα μήκη ανακυκλώνοντας ή επαναλαμβάνοντας το μικρότερο διάνυσμα. Μπορούμε να το δούμε σε λειτουργία πιο εύκολα εάν δημιουργήσουμε μερικά διανύσματα εκτός κάποιου πλαισίου δεδομένων:

x <- c(1, 2, 10, 20)
x / 5
#> [1] 0.2 0.4 2.0 4.0
# είναι συντομογραφία για το
x / c(5, 5, 5, 5)
#> [1] 0.2 0.4 2.0 4.0

Γενικά, θέλετε να ανακυκλώσετε μόνο μεμονωμένους αριθμούς (δηλαδή διανύσματα μήκους 1), αλλά η R θα ανακυκλώσει οποιοδήποτε διάνυσμα μικρότερου μήκους. Συνήθως (αλλά όχι πάντα) σας δίνει μία προειδοποίηση εάν το μεγαλύτερο διάνυσμα δεν είναι πολλαπλάσιο του μικρότερου:

x * c(1, 2)
#> [1]  1  4 10 40
x * c(1, 2, 3)
#> Warning in x * c(1, 2, 3): longer object length is not a multiple of shorter
#> object length
#> [1]  1  4 30 20

Αυτοί οι κανόνες ανακύκλωσης εφαρμόζονται επίσης σε λογικές συγκρίσεις (==, <, <=, >, >=, !=) και μπορούν να οδηγήσουν σε ένα απροσδόκητο αποτέλεσμα εάν χρησιμοποιήσετε κατά λάθος το == αντί για το %in% και το πλαίσιο δεδομένων έχει έναν μη αναμενόμενο αριθμό γραμμών. Για παράδειγμα, πάρτε τον παρακάτω κώδικα ο οποίος προσπαθεί να βρει όλες τις πτήσεις τον Ιανουάριο και τον Φεβρουάριο:

flights |> 
  filter(month == c(1, 2))
#> # A tibble: 25,977 × 19
#>    year month   day dep_time sched_dep_time dep_delay arr_time sched_arr_time
#>   <int> <int> <int>    <int>          <int>     <dbl>    <int>          <int>
#> 1  2013     1     1      517            515         2      830            819
#> 2  2013     1     1      542            540         2      923            850
#> 3  2013     1     1      554            600        -6      812            837
#> 4  2013     1     1      555            600        -5      913            854
#> 5  2013     1     1      557            600        -3      838            846
#> 6  2013     1     1      558            600        -2      849            851
#> # ℹ 25,971 more rows
#> # ℹ 11 more variables: arr_delay <dbl>, carrier <chr>, flight <int>, …

Ο κώδικας εκτελείται χωρίς σφάλμα, αλλά δεν επιστρέφει αυτό που θέλετε. Λόγω των κανόνων ανακύκλωσης, βρίσκει πτήσεις σε μονές γραμμές που αναχώρησαν τον Ιανουάριο και πτήσεις σε ζυγές γραμμές που αναχώρησαν τον Φεβρουάριο. Και δυστυχώς δεν υπάρχει καμία προειδοποίηση επειδή το σύνολο δεδομένων flights έχει ζυγό αριθμό γραμμών.

Για να σας προστατεύσουν από αυτόν τον τύπο αθόρυβης αποτυχίας, οι περισσότερες συναρτήσεις του tidyverse χρησιμοποιούν μία πιο αυστηρή μορφή ανακύκλωσης, η οποία ανακυκλώνει μόνο μεμονωμένες τιμές. Δυστυχώς, εδώ, ή ακόμα και σε πολλές άλλες περιπτώσεις, αυτό δεν βοηθά, γιατί ο κύριος υπολογισμός εκτελείται από τον βασικό τελεστή του βασικού πακέτου λειτουργιών της R, ==, και όχι από την filter().

13.4.2 Ελάχιστο και μέγιστο

Οι αριθμητικές συναρτήσεις λειτουργούν με ζεύγη μεταβλητών. Δύο στενά συνδεδεμένες συναρτήσεις είναι οι pmin() και pmax(), οι οποίες όταν τους δίνονται δύο ή περισσότερες μεταβλητές θα επιστρέψουν τη μικρότερη ή μεγαλύτερη τιμή σε κάθε γραμμή:

df <- tribble(
  ~x, ~y,
  1,  3,
  5,  2,
  7, NA,
)

df |> 
  mutate(
    min = pmin(x, y, na.rm = TRUE),
    max = pmax(x, y, na.rm = TRUE)
  )
#> # A tibble: 3 × 4
#>       x     y   min   max
#>   <dbl> <dbl> <dbl> <dbl>
#> 1     1     3     1     3
#> 2     5     2     2     5
#> 3     7    NA     7     7

Σημειώστε ότι αυτές διαφέρουν από τις συναρτήσεις σύνοψης min() και max() οι οποίες παίρνουν πολλαπλές παρατηρήσεις και επιστρέφουν μόνο μία τιμή. Μπορείτε να πείτε ότι έχετε χρησιμοποιήσει την λάθος συνάρτηση όταν όλα τα ελάχιστα και όλα τα μέγιστα έχουν την ίδια τιμή:

df |> 
  mutate(
    min = min(x, y, na.rm = TRUE),
    max = max(x, y, na.rm = TRUE)
  )
#> # A tibble: 3 × 4
#>       x     y   min   max
#>   <dbl> <dbl> <dbl> <dbl>
#> 1     1     3     1     7
#> 2     5     2     1     7
#> 3     7    NA     1     7

13.4.3 Αριθμητική υπολοίπων

Η αριθμητική υπολοίπων είναι η τεχνική ονομασία για τον τύπο μαθηματικών που κάνατε πριν μάθετε για τα δεκαδικά ψηφία, δηλαδή τη διαίρεση που δίνει έναν ακέραιο αριθμό και ένα υπόλοιπο. Στην R, το %/% κάνει διαίρεση ακεραίων και το %% υπολογίζει το υπόλοιπο:

1:10 %/% 3
#>  [1] 0 0 1 1 1 2 2 2 3 3
1:10 %% 3
#>  [1] 1 2 0 1 2 0 1 2 0 1

Η αριθμητική υπολοίπων είναι χρήσιμη για το σύνολο δεδομένων flights, καθώς μπορούμε να τη χρησιμοποιήσουμε για να αποσυνθέσουμε τη μεταβλητή sched_dep_time σε hour (ώρα) και minute (λεπτό):

flights |> 
  mutate(
    hour = sched_dep_time %/% 100,
    minute = sched_dep_time %% 100,
    .keep = "used"
  )
#> # A tibble: 336,776 × 3
#>   sched_dep_time  hour minute
#>            <int> <dbl>  <dbl>
#> 1            515     5     15
#> 2            529     5     29
#> 3            540     5     40
#> 4            545     5     45
#> 5            600     6      0
#> 6            558     5     58
#> # ℹ 336,770 more rows

Μπορούμε να τη συνδυάσουμε με το κόλπο που βασίζεται στην mean(is.na(x)) από την Ενότητα 12.4, για να δούμε πώς το ποσοστό των ακυρωμένων πτήσεων διαφέρει κατά τη διάρκεια της ημέρας. Τα αποτελέσματα εμφανίζονται στο Σχήμα 13.1.

flights |> 
  group_by(hour = sched_dep_time %/% 100) |> 
  summarize(prop_cancelled = mean(is.na(dep_time)), n = n()) |> 
  filter(hour > 1) |> 
  ggplot(aes(x = hour, y = prop_cancelled)) +
  geom_line(color = "grey50") + 
  geom_point(aes(size = n))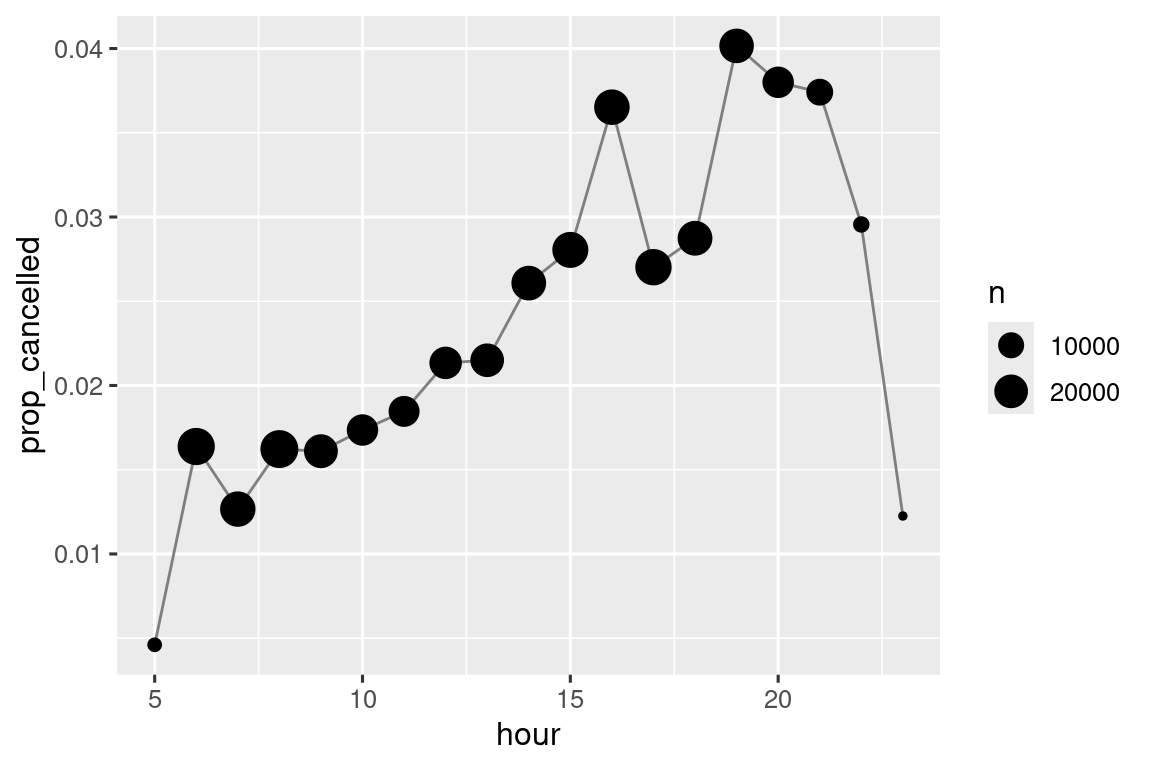

Ένα διάγραμμα γραμμών που δείχνει πως αλλάζει η αναλογία των ακυρωμένων πτήσεων στη διάρκεια της μέρας. Αυτό το ποσοστό ξεκινά χαμηλά, κοντά στο 0,5% στις 6πμ, και στη συνέχεια αυξάνεται σταθερά στη διάρκεια της ημέρας, μέχρι να φτάσει στο 4% στις 7μμ. Στη συνέχεια πέφτει γρήγορα, φτάνοντας κοντά στο 1% μέχρι τα μεσάνυχτα. — Σχήμα 13.1: Ένα διάγραμμα γραμμής με την προγραμματισμένη ώρα αναχώρησης στον άξονα x και την αναλογία ακυρωμένων πτήσεων στον άξονα y. Οι ακυρώσεις φαίνεται να συσσωρεύονται κατά τη διάρκεια της ημέρας μέχρι τις 8μμ, ενώ οι πολύ καθυστερημένες πτήσεις είναι πολύ λιγότερο πιθανό να ακυρωθούν.

13.4.4 Λογάριθμοι

Οι λογάριθμοι είναι ένας απίστευτα χρήσιμος μετασχηματισμός για την αντιμετώπιση δεδομένων που κυμαίνονται σε πολλαπλές τάξεις μεγέθους και τη μετατροπή της εκθετικής αύξησης σε γραμμική αύξηση. Στην R, έχετε να επιλέξετε μεταξύ τριών συναρτήσεων λογαρίθμων: log() (τον φυσικό λογάριθμο, με βάση την σταθερά e), log2() (με βάση το 2) και log10() (με βάση το 10). Συνιστούμε τη χρήση της log2() ή log10(). Η log2() ερμηνεύετε εύκολα καθώς μία διαφορά μονάδας στην λογαριθμική κλίμακα αντιστοιχεί σε διπλασιασμό στην αρχική κλίμακα και μία διαφορά -1 αντιστοιχεί στο μισό της αρχικής. Η log10() είναι εύκολο να μετασχηματιστεί ξανά επειδή (π.χ.) το 3 είναι 10^3 = 1000. Το αντίστροφο της log() είναι η exp(). Για να υπολογίσετε το αντίστροφο της log2() ή της log10() θα χρειαστεί να χρησιμοποιήσετε το 2^ ή το 10^.

13.4.5 Στρογγυλοποίηση

Χρησιμοποιήστε την round(x) για να στρογγυλοποιήσετε έναν αριθμό στον πλησιέστερο ακέραιο:

round(123.456)
#> [1] 123

Μπορείτε να ελέγξετε την ακρίβεια της στρογγυλοποίησης με το δεύτερο όρισμα, το digits. Η round(x, digits) στρογγυλοποιείται στο πλησιέστερο 10^-n οπότε το digits = 2 θα στρογγυλοποιηθεί στο πλησιέστερο 0,01. Αυτός ο ορισμός είναι χρήσιμος επειδή υπονοεί ότι το round(x, -3) θα στρογγυλοποιηθεί στην πλησιέστερη χιλιάδα, κάτι που όντως συμβαίνει:

round(123.456, 2)  # δύο ψηφία
#> [1] 123.46
round(123.456, 1)  # ένα ψηφίο
#> [1] 123.5
round(123.456, -1) # στρογγυλοποίηση στη πλησιέστερη δεκάδα
#> [1] 120
round(123.456, -2) # στρογγυλοποίηση στη πλησιέστερη χιλιάδα
#> [1] 100

Εκ πρώτης όψεως, φαίνεται να υπάρχει κάτι παράξενο με την round():

round(c(1.5, 2.5))
#> [1] 2 2

Η round() χρησιμοποιεί κάτι που είναι γνωστό ως “στρογγυλοποίηση μισού στον πλησιέστερο ζυγού” ή τραπεζική στρογγυλοποίηση: εάν ένας αριθμός βρίσκεται στη μέση μεταξύ δύο ακεραίων, θα στρογγυλοποιηθεί στον ζυγό ακέραιο. Αυτή είναι μία καλή στρατηγική γιατί διατηρεί τη στρογγυλοποίηση αμερόληπτη: τα μισά από όλα τα 0,5 στρογγυλοποιούνται ένα προς τα πάνω και τα μισά στρογγυλοποιούνται ένα προς τα κάτω.

Η round() συνδυάζεται με την floor() που στρογγυλοποιεί πάντα προς τα κάτω και την ceiling() που στρογγυλοποιεί πάντα προς τα πάνω:

x <- 123.456

floor(x)
#> [1] 123
ceiling(x)
#> [1] 124

Οι συναρτήσεις αυτές δεν έχουν όρισμα digits, για να μπορείτε να στρογγυλοποιήσετε προς τα κάτω και προς τα πάνω:

# Στρογγυλοποίηση προς τα κάτω στα πλησιέστερα δύο ψηφία
floor(x / 0.01) * 0.01
#> [1] 123.45
# Στρογγυλοποίηση προς τα πάνω στα πλησιέστερα δύο ψηφία
ceiling(x / 0.01) * 0.01
#> [1] 123.46

Μπορείτε να χρησιμοποιήσετε την ίδια τεχνική εάν θέλετε να χρησιμοποιήσετε την round() σε ένα πολλαπλάσιο κάποιου άλλου αριθμού:

# Στρογγυλοποίηση στο πλησιέστερο πολλαπλάσιο του 4
round(x / 4) * 4
#> [1] 124

# Στρογγυλοποίηση στο πλησιέστερο τεταρτημόριο (0.25)
round(x / 0.25) * 0.25
#> [1] 123.5

13.4.6 Τοποθετώντας αριθμούς σε εύρη

Χρησιμοποιήστε την cut()¹ για να χωρίσετε ένα αριθμητικό διάνυσμα σε διακριτές κατηγορίες (διαδικασία γνωστή και ως binning):

x <- c(1, 2, 5, 10, 15, 20)
cut(x, breaks = c(0, 5, 10, 15, 20))
#> [1] (0,5]   (0,5]   (0,5]   (5,10]  (10,15] (15,20]
#> Levels: (0,5] (5,10] (10,15] (15,20]

Τα διαχωριστικά (breaks) δεν χρειάζεται να είναι ομοιόμορφα:

cut(x, breaks = c(0, 5, 10, 100))
#> [1] (0,5]    (0,5]    (0,5]    (5,10]   (10,100] (10,100]
#> Levels: (0,5] (5,10] (10,100]

Μπορείτε προαιρετικά να δώσετε τις δικές σας ετικέτες (labels). Σημειώστε ότι θα πρέπει να υπάρχει μία ετικέτα λιγότερη από τα διαχωριστικά (breaks).

cut(x, 
  breaks = c(0, 5, 10, 15, 20), 
  labels = c("sm", "md", "lg", "xl")
)
#> [1] sm sm sm md lg xl
#> Levels: sm md lg xl

Οποιεσδήποτε τιμές εκτός του εύρους των διαχωριστικών θα γίνουν NA:

y <- c(NA, -10, 5, 10, 30)
cut(y, breaks = c(0, 5, 10, 15, 20))
#> [1] <NA>   <NA>   (0,5]  (5,10] <NA>  
#> Levels: (0,5] (5,10] (10,15] (15,20]

Δείτε τις οδηγίες και για άλλα χρήσιμα ορίσματα, όπως το right και το include.lowest, τα οποία ελέγχουν εάν τα διαστήματα είναι [a, b) ή (a, b] και εάν το χαμηλότερο διάστημα πρέπει να είναι [a, b].

13.4.7 Συσσωρευτικά και κυλιόμενα σύνολα

Το βασικό πακέτο λειτουργιών της R παρέχει τις συναρτήσεις cumsum(), cumprod(), cummin(), cummax() για κυλιόμενα ή συσσωρευτικά αθροίσματα, γινόμενα, ελάχιστα και μέγιστα. Η dplyr παρέχει την cummean() για συσσωρευτικούς μέσους. Στην πράξη, τα συσσωρευτικά αθροίσματα τείνουν να προκύπτουν περισσότερο:

x <- 1:10
cumsum(x)
#>  [1]  1  3  6 10 15 21 28 36 45 55

Εάν χρειάζεστε πιο σύνθετα κυλιόμενα σύνολα, δοκιμάστε το πακέτο slider.

13.4.8 Ασκήσεις

Εξηγήστε με λόγια τι κάνει κάθε γραμμή του κώδικα που χρησιμοποιήθηκε για τη δημιουργία του Σχήμα 13.1.
Ποιες τριγωνομετρικές συναρτήσεις παρέχει η R;
Μαντέψτε μερικά ονόματα και αναζητήστε την τεκμηρίωση. Χρησιμοποιούν μοίρες ή ακτίνια;
Προς το παρόν, οι στήλες dep_time και sched_dep_time είναι χρήσιμες για να τις εξετάσει κανείς, αλλά είναι δύσκολο να χρησιμοποιηθούν σε υπολογισμούς, επειδή δεν είναι πραγματικά συνεχείς αριθμοί. Μπορείτε να παρατηρήσετε αυτό το βασικό πρόβλημα εκτελώντας τον παρακάτω κώδικα: υπάρχει ένα κενό μεταξύ κάθε ώρας.
```
flights |> 
  filter(month == 1, day == 1) |> 
  ggplot(aes(x = sched_dep_time, y = dep_delay)) +
  geom_point()
```
Μετατρέψτε τες σε μία πιο πραγματική αναπαράσταση του χρόνου (είτε κλασματικές ώρες είτε λεπτά μετά τα μεσάνυχτα).
Στρογγυλοποιήστε τις dep_time και arr_time στα πιο κοντινά πέντε λεπτά.

13.5 Γενικοί μετασχηματισμοί

Οι ακόλουθες ενότητες περιγράφουν ορισμένους γενικούς μετασχηματισμούς που χρησιμοποιούνται συχνά με αριθμητικά διανύσματα, αλλά μπορούν να εφαρμοστούν σε όλους τους άλλους τύπους στηλών.

13.5.1 Κατατάξεις

Η dplyr παρέχει μία σειρά από συναρτήσεις κατάταξης εμπνευσμένες από την SQL, αλλά θα πρέπει πάντα να ξεκινάτε με την dplyr::min_rank(). Αυτή χρησιμοποιεί την συνηθισμένη μέθοδο για τον χειρισμό της ισοπαλίας, π.χ., 1ος, 2ος, 2ος, 4ος.

x <- c(1, 2, 2, 3, 4, NA)
min_rank(x)
#> [1]  1  2  2  4  5 NA

Σημειώστε ότι οι μικρότερες τιμές λαμβάνουν τις χαμηλότερες κατατάξεις. Χρησιμοποιήστε την desc(x) για να δώσετε στις μεγαλύτερες τιμές τις μικρότερες κατατάξεις:

min_rank(desc(x))
#> [1]  5  3  3  2  1 NA

Εάν η min_rank() δεν κάνει αυτό που χρειάζεστε, εξερευνήστε τις παραλλαγές dplyr::row_number(), dplyr::dense_rank(), dplyr::percent_rank() και dplyr:: cume_dist(). Δείτε τις οδηγίες για λεπτομέρειες.

df <- tibble(x = x)
df |> 
  mutate(
    row_number = row_number(x),
    dense_rank = dense_rank(x),
    percent_rank = percent_rank(x),
    cume_dist = cume_dist(x)
  )
#> # A tibble: 6 × 5
#>       x row_number dense_rank percent_rank cume_dist
#>   <dbl>      <int>      <int>        <dbl>     <dbl>
#> 1     1          1          1         0          0.2
#> 2     2          2          2         0.25       0.6
#> 3     2          3          2         0.25       0.6
#> 4     3          4          3         0.75       0.8
#> 5     4          5          4         1          1  
#> 6    NA         NA         NA        NA         NA

Μπορείτε να πετύχετε ίδια αποτελέσματα με πολλές από τις παραπάνω συναρτήσεις επιλέγοντας την κατάλληλη τιμή στο όρισμα ties.method στην rank() του βασικού πακέτου λειτουργιών της R. Πιθανότατα θα θέλετε επίσης να ορίσετε το na.last = "keep" για να διατηρήσετε τα NA ως NA.

Η row_number() μπορεί επίσης να χρησιμοποιηθεί χωρίς ορίσματα όταν βρίσκεται μέσα σε μία συνάρτηση της dplyr. Σε αυτήν την περίπτωση, θα δώσει τον αριθμό της “τρέχουσας” γραμμής. Επιπλέον, όταν συνδυαστεί με το %% ή το %/%, μπορεί να γίνει ένα χρήσιμο εργαλείο για τη διαίρεση δεδομένων σε ομάδες παρόμοιου μεγέθους:

df <- tibble(id = 1:10)

df |> 
  mutate(
    row0 = row_number() - 1,
    three_groups = row0 %% 3,
    three_in_each_group = row0 %/% 3
  )
#> # A tibble: 10 × 4
#>      id  row0 three_groups three_in_each_group
#>   <int> <dbl>        <dbl>               <dbl>
#> 1     1     0            0                   0
#> 2     2     1            1                   0
#> 3     3     2            2                   0
#> 4     4     3            0                   1
#> 5     5     4            1                   1
#> 6     6     5            2                   1
#> # ℹ 4 more rows

13.5.2 Ορίσματα μετατόπισης

Οι dplyr::lead() και dplyr::lag() σας επιτρέπουν να αναφερθείτε στις τιμές ακριβώς πριν ή αμέσως μετά την “τρέχουσα” τιμή. Επιστρέφουν ένα διάνυσμα του ίδιου μήκους με την είσοδο, με πρόσθετες τιμές NA στην αρχή ή στο τέλος:

x <- c(2, 5, 11, 11, 19, 35)
lag(x)
#> [1] NA  2  5 11 11 19
lead(x)
#> [1]  5 11 11 19 35 NA

Το x - lag(x) σας δίνει τη διαφορά μεταξύ της τρέχουσας και της προηγούμενης τιμής.
```
x - lag(x)
#> [1] NA  3  6  0  8 16
```
Το x == lag(x) σας λέει πότε αλλάζει η τρέχουσα τιμή.
```
x == lag(x)
#> [1]    NA FALSE FALSE  TRUE FALSE FALSE
```

Μπορείτε να πάρετε τιμές πριν και μετά, κατά περισσότερες από μία θέσεις, χρησιμοποιώντας το δεύτερο όρισμα, n.

13.5.3 Διαδοχικά αναγνωριστικά

Μερικές φορές θέλετε να ξεκινήσετε μία νέα ομάδα κάθε φορά που κάποιο συμβάν λαμβάνει χώρα. Για παράδειγμα, όταν έχετε να κάνετε με δεδομένα ιστοτόπου, είναι σύνηθες να θέλετε να χωρίσετε τα συμβάντα σε περιόδους σύνδεσης, ξεκινώντας μία νέα περίοδο μετά από ένα κενό άνω των x λεπτών από την τελευταία δραστηριότητα. Για παράδειγμα, φανταστείτε ότι έχετε τις στιγμές που κάποιος επισκέφτηκε έναν ιστότοπο:

events <- tibble(
  time = c(0, 1, 2, 3, 5, 10, 12, 15, 17, 19, 20, 27, 28, 30)
)

Έχετε υπολογίσει το χρόνο μεταξύ κάθε γεγονότος και έχετε βρει εάν υπάρχει κάποιο κενό αρκετά μεγάλο για να πληροί τις προϋποθέσεις:

events <- events |> 
  mutate(
    diff = time - lag(time, default = first(time)),
    has_gap = diff >= 5
  )
events
#> # A tibble: 14 × 3
#>    time  diff has_gap
#>   <dbl> <dbl> <lgl>  
#> 1     0     0 FALSE  
#> 2     1     1 FALSE  
#> 3     2     1 FALSE  
#> 4     3     1 FALSE  
#> 5     5     2 FALSE  
#> 6    10     5 TRUE   
#> # ℹ 8 more rows

Αλλά πώς πηγαίνουμε από αυτό το λογικό διάνυσμα σε κάτι που μπορούμε να εφαρμόσουμε την group_by();
H cumsum(), από την Ενότητα 13.4.7, σώζει την κατάσταση, καθώς όταν η has_gap είναι TRUE, θα αυξήσει την group κατά ένα (Ενότητα 12.4.2):

events |> mutate(
  group = cumsum(has_gap)
)
#> # A tibble: 14 × 4
#>    time  diff has_gap group
#>   <dbl> <dbl> <lgl>   <int>
#> 1     0     0 FALSE       0
#> 2     1     1 FALSE       0
#> 3     2     1 FALSE       0
#> 4     3     1 FALSE       0
#> 5     5     2 FALSE       0
#> 6    10     5 TRUE        1
#> # ℹ 8 more rows

Μία άλλη προσέγγιση για τη δημιουργία μεταβλητών ομαδοποίησης είναι η consecutive_id(), η οποία ξεκινά μία νέα ομάδα κάθε φορά που αλλάζει ένα από τα ορίσματά της. Για παράδειγμα, εμπνευσμένο από αυτή την ερώτηση στο stackoverflow, φανταστείτε ότι έχετε ένα πλαίσιο δεδομένων με επαναλαμβανόμενες τιμές:

df <- tibble(
  x = c("a", "a", "a", "b", "c", "c", "d", "e", "a", "a", "b", "b"),
  y = c(1, 2, 3, 2, 4, 1, 3, 9, 4, 8, 10, 199)
)

Εάν θέλετε να διατηρήσετε την πρώτη γραμμή από κάθε επαναλαμβανόμενο x, μπορείτε να χρησιμοποιήσετε τις group_by(), consecutive_id() και slice_head():

df |> 
  group_by(id = consecutive_id(x)) |> 
  slice_head(n = 1)
#> # A tibble: 7 × 3
#> # Groups:   id [7]
#>   x         y    id
#>   <chr> <dbl> <int>
#> 1 a         1     1
#> 2 b         2     2
#> 3 c         4     3
#> 4 d         3     4
#> 5 e         9     5
#> 6 a         4     6
#> # ℹ 1 more row

13.5.4 Ασκήσεις

Βρείτε τις 10 πτήσεις με τις περισσότερες καθυστερήσεις χρησιμοποιώντας μία συνάρτηση κατάταξης. Πώς θέλετε να χειριστείτε τις ισοπαλίες;
Διαβάστε προσεκτικά τις οδηγίες για την min_rank().
Ποιο αεροπλάνο (tailnum) έχει το χειρότερο ρεκόρ για το εάν είναι στην ώρα του;
Ποια ώρα της ημέρας πρέπει να πετάξετε αν θέλετε να αποφύγετε όσο το δυνατόν περισσότερες καθυστερήσεις;
Τι κάνει το flights |> group_by(dest) |> filter(row_number() < 4);
Τι κάνει το flights |> group_by(dest) |> filter(row_number(dep_delay) < 4);
Για κάθε προορισμό, υπολογίστε τα συνολικά λεπτά καθυστέρησης. Για κάθε πτήση, υπολογίστε το ποσοστό της συνολικής καθυστέρησης για τον προορισμό της.
Οι καθυστερήσεις συνήθως συσχετίζονται χρονικά: ακόμη και όταν επιλυθεί το πρόβλημα που προκάλεσε την αρχική καθυστέρηση, οι μεταγενέστερες πτήσεις καθυστερούν για να επιτραπεί η αναχώρηση των προηγούμενων πτήσεων. Χρησιμοποιώντας την lag(), εξερευνήστε πώς η μέση καθυστέρηση πτήσης για μία ώρα σχετίζεται με τη μέση καθυστέρηση για την προηγούμενη ώρα.
```
flights |> 
  mutate(hour = dep_time %/% 100) |> 
  group_by(year, month, day, hour) |> 
  summarize(
    dep_delay = mean(dep_delay, na.rm = TRUE),
    n = n(),
    .groups = "drop"
  ) |> 
  filter(n > 5)
```
Παρατηρήστε κάθε προορισμό. Μπορείτε να βρείτε πτήσεις που είναι ύποπτα γρήγορες (δηλαδή πτήσεις που παρουσιάζουν ένα πιθανό σφάλμα εισαγωγής δεδομένων);
Υπολογίστε τον χρόνο που βρίσκεται στον αέρα μία πτήση, σε σχέση με τη συντομότερη πτήση προς αυτόν τον προορισμό. Ποιες πτήσεις καθυστέρησαν περισσότερο στον αέρα;
Βρείτε όλους τους προορισμούς που πραγματοποιούν πτήσεις από τουλάχιστον δύο εταιρίες. Χρησιμοποιήστε αυτούς τους προορισμούς για να καταλήξετε σε μία σχετική κατάταξη των αερομεταφορέων με βάση την απόδοσή τους για τον ίδιο προορισμό.

13.6 Αριθμητικές συνόψεις

Η χρήση των καταμετρήσεων, των μέσων και των αθροισμάτων που έχουμε ήδη παρουσιάσει μπορεί να σας βοηθήσει αρκετά, αλλά η R παρέχει πολλές άλλες χρήσιμες συναρτήσεις σύνοψης. Παρακάτω υπάρχουν επιλογές που μπορεί να σας φανούν χρήσιμες.

13.6.1 Κεντρική θέση

Μέχρι στιγμής, χρησιμοποιούσαμε κυρίως την mean() για να συνοψίσουμε το κέντρο ενός διανύσματος τιμών. Όπως είδαμε στην Ενότητα 3.6, επειδή ο μέσος όρος είναι το άθροισμα διαιρούμενο με το πλήθος, είναι ευαίσθητο ακόμη και σε λίγες ασυνήθιστα υψηλές ή χαμηλές τιμές. Μία εναλλακτική λύση είναι να χρησιμοποιήσετε την median(), η οποία βρίσκει μία τιμή που βρίσκεται στη “μέση” του διανύσματος, δηλαδή το 50% των τιμών είναι πάνω από αυτό και το άλλο 50% είναι κάτω από αυτό. Ανάλογα με το σχήμα της κατανομής της μεταβλητής που σας ενδιαφέρει, ο καλύτερος υπολογισμός του κέντρου μπορεί να γίνει είτε μέσα από τον μέσο όρο είτε μέσα από την διάμεσο. Για παράδειγμα, για συμμετρικές κατανομές αναφέρουμε γενικά τη μέση τιμή ενώ για λοξές (ασύμμετρες) κατανομές συνήθως αναφέρουμε τη διάμεσο.

Το Σχήμα 13.2 συγκρίνει τη μέση με τη διάμεση καθυστέρηση αναχώρησης (σε λεπτά) για κάθε προορισμό. Η διάμεση καθυστέρηση είναι πάντα μικρότερη από τη μέση καθυστέρηση, επειδή οι πτήσεις μερικές φορές αναχωρούν με καθυστέρηση πολλών ωρών, αλλά ποτέ δεν αναχωρούν πολλές ώρες νωρίτερα.

flights |>
  group_by(year, month, day) |>
  summarize(
    mean = mean(dep_delay, na.rm = TRUE),
    median = median(dep_delay, na.rm = TRUE),
    n = n(),
    .groups = "drop"
  ) |> 
  ggplot(aes(x = mean, y = median)) + 
  geom_abline(slope = 1, intercept = 0, color = "white", linewidth = 2) +
  geom_point()

Όλα τα σημεία βρίσκονται κάτω από τη γραμμή των 45°, που σημαίνει ότι η διάμεση καθυστέρηση είναι πάντα μικρότερη από τη μέση καθυστέρηση. Τα περισσότερα σημεία ομαδοποιούνται σε μια πυκνή περιοχή με μέση τιμή [0, 20] και διάμεσο [0, 5]. Καθώς η μέση καθυστέρηση αυξάνεται, η διασπορά της διαμέσου αυξάνεται επίσης. Υπάρχουν δύο ακραία σημεία, με μέση τιμή ~60, διάμεσο ~50 και μέση τιμή ~85, διάμεσο ~55. — Σχήμα 13.2: Ένα διάγραμμα διασποράς που δείχνει τις διαφορές της σύνοψης της ημερήσιας καθυστέρησης αναχώρησης με την διάμεσο αντί για τον μέσο όρο.

Μπορεί επίσης να αναρωτιέστε για την επικρατούσα τιμή ή την πιο συχνή τιμή. Αυτή είναι μία σύνοψη που λειτουργεί καλά μόνο για πολύ απλές περιπτώσεις (γι’ αυτό μπορεί να την έχετε μάθει στο λύκειο), αλλά δεν λειτουργεί καλά για πολλά πραγματικά σύνολα δεδομένων. Εάν τα δεδομένα είναι διακριτά, μπορεί να υπάρχουν πολλαπλές κοινές τιμές και εάν τα δεδομένα είναι συνεχή, μπορεί να μην υπάρχει πιο κοινή τιμή επειδή κάθε τιμή είναι πάντα ελαφρώς διαφορετική. Για αυτούς τους λόγους, η επικρατούσα τιμή τείνει να μην χρησιμοποιείται από στατιστικολόγους και δεν περιλαμβάνεται σε κάποια συνάρτηση του βασικού πακέτου λειτουργιών της R².

13.6.2 Ελάχιστα, μέγιστα και ποσοστηµόρια

Τι γίνεται αν ενδιαφέρεστε για άλλες θέσεις εκτός από το κέντρο;
Οι min() και max() θα σας δώσουν τις μεγαλύτερες και τις μικρότερες τιμές αντίστοιχα. Ένα άλλο ισχυρό εργαλείο είναι η συνάρτηση quantile() που είναι μία γενίκευση της διάμεσης τιμής: η quantile(x, 0.25) θα βρει την τιμή του x που είναι μεγαλύτερη από το 25% των τιμών, η quantile(x, 0.5) ισοδυναμεί με τη διάμεσο και η quantile(x, 0.95) θα βρει την τιμή που είναι μεγαλύτερη από το 95% των τιμών.

Για το σύνολο δεδομένων flights, ίσως θελήσετε να εξετάσετε το 95% των καθυστερήσεων και όχι τον μέγιστο αριθμό, καθώς θα αγνοήσει το 5% των περισσότερων καθυστερημένων πτήσεων, οι οποίες μπορεί να είναι αρκετά ακραίες.

flights |>
  group_by(year, month, day) |>
  summarize(
    max = max(dep_delay, na.rm = TRUE),
    q95 = quantile(dep_delay, 0.95, na.rm = TRUE),
    .groups = "drop"
  )
#> # A tibble: 365 × 5
#>    year month   day   max   q95
#>   <int> <int> <int> <dbl> <dbl>
#> 1  2013     1     1   853  70.1
#> 2  2013     1     2   379  85  
#> 3  2013     1     3   291  68  
#> 4  2013     1     4   288  60  
#> 5  2013     1     5   327  41  
#> 6  2013     1     6   202  51  
#> # ℹ 359 more rows

13.6.3 Έκταση

Μερικές φορές δεν ενδιαφέρεστε τόσο για το πού βρίσκεται το μεγαλύτερο μέρος των δεδομένων, αλλά για το πώς εκτείνονται τα δεδομένα. Δύο συνόψεις που χρησιμοποιούνται συνήθως είναι η τυπική απόκλιση, sd(x), και το ενδοτεταρτημοριακό εύρος, IQR(). Δεν θα εξηγήσουμε την sd() εδώ, καθώς πιθανώς το γνωρίζετε ήδη, η IQR() όμως μπορεί να είναι νέα για εσάς — στην ουσία είναι το αποτέλεσμα του quantile(x, 0.75) - quantile(x, 0.25) και σας δίνει το εύρος που περιέχει το μεσαίο 50% των δεδομένων.

Μπορούμε να το χρησιμοποιήσουμε για να αποκαλύψουμε μία μικρή ιδιορρυθμία στα δεδομένα του flights. Μπορεί να περιμένετε ότι η έκταση της απόστασης μεταξύ προέλευσης και προορισμού θα είναι μηδενική, καθώς τα αεροδρόμια βρίσκονται πάντα στο ίδιο σημείο. Ο παρακάτω κώδικας όμως αποκαλύπτει κάτι περίεργο για το αεροδρόμιο EGE:

flights |> 
  group_by(origin, dest) |> 
  summarize(
    distance_iqr = IQR(distance), 
    n = n(),
    .groups = "drop"
  ) |> 
  filter(distance_iqr > 0)
#> # A tibble: 2 × 4
#>   origin dest  distance_iqr     n
#>   <chr>  <chr>        <dbl> <int>
#> 1 EWR    EGE              1   110
#> 2 JFK    EGE              1   103

13.6.4 Κατανομές

Αξίζει να θυμάστε ότι όλα τα στατιστικά στοιχεία σύνοψης που περιγράφονται παραπάνω είναι ένας τρόπος συμπύκνωσης της κατανομής σε έναν μόνο αριθμό. Αυτό σημαίνει ότι είναι θεμελιωδώς αναγωγικά και αν επιλέξετε λάθος σύνοψη, μπορείτε εύκολα να χάσετε σημαντικές διαφορές μεταξύ ομάδων. Γι’ αυτό, είναι πάντα καλή ιδέα να οπτικοποιείτε τη κατανομή προτού αποφασίσετε για τα στατιστικά σύνοψης σας.

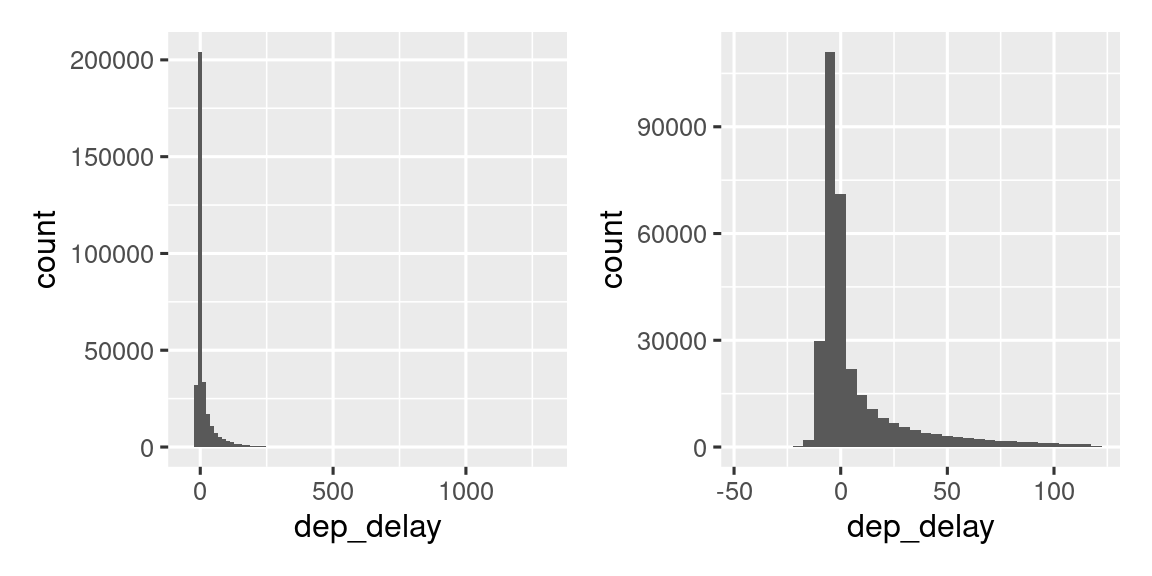
Το Σχήμα 13.3 δείχνει τη συνολική κατανομή των καθυστερήσεων αναχώρησης. Η κατανομή είναι τόσο λοξή που πρέπει να εστιάσουμε κατάλληλα για να δούμε το μεγαλύτερο μέρος των δεδομένων. Αυτό υποδηλώνει ότι ο μέσος όρος είναι απίθανο να δώσει μία καλή σύνοψη και ίσως προτιμήσουμε τη διάμεσο.

Δυο ιστογράμματα της μεταβλητής `dep_delay`. Στα αριστερά, είναι αρκετά δύσκολο να δεότε οποιοδήποτε μοτίβο πέρα από το ότι υπάρχει μια πολύ μεγάλη αύξηση γύρω από το μηδέν, ενώ οι μπάρες μειώνονται γρήγορα σε ύψος, με αποτέλεσμα για το μεγαλύτερο μέρος του διαγράμματος να μην μπορείτε να δείτε καν μπάρες, μιας και είναι πολύ χαμηλές για να παρατηρηθούν. Στα δεξιά, όπου έχουμε απορρίψει καθυστερήσεις μεγαλύτερες από δύο ώρες, μπορούμε να δούμε ότι αυτή η αύξη συμβαίνει ελαφρώς κάτω από το μηδέν (που σημαίνει ότι οι περισσότερες πτήσεις αναχωρούν μερικά λεπτά νωρίτερα), ωστόσο υπάρχει μια αρκετά απότομη πτώση στη συνέχεια. — Σχήμα 13.3: (Αριστερά) Το ιστόγραμμα όλων των δεδομένων είναι εξαιρετικά λοξό, καθιστώντας την λήψη πληροφοριών δύσκολη. (Δεξιά) Η εστίαση στις καθυστερήσεις μικρότερες των δύο ωρών καθιστά δυνατή την εξερεύνηση του μεγαλύτερο μέρος των παρατηρήσεων.

Είναι επίσης καλή ιδέα να ελέγξετε ότι οι κατανομές των υποομάδων μοιάζουν με το σύνολο. Στο ακόλουθο διάγραμμα βλέπουμε να επικαλύπτονται 365 πολύγωνα συχνότητας της μεταβλητής dep_delay, ένα για κάθε ημέρα. Οι κατανομές φαίνεται να ακολουθούν ένα κοινό μοτίβο, υποδηλώνοντας ότι είναι καλό να χρησιμοποιείτε την ίδια σύνοψη για κάθε μέρα.

flights |>
  filter(dep_delay < 120) |> 
  ggplot(aes(x = dep_delay, group = interaction(day, month))) + 
  geom_freqpoly(binwidth = 5, alpha = 1/5)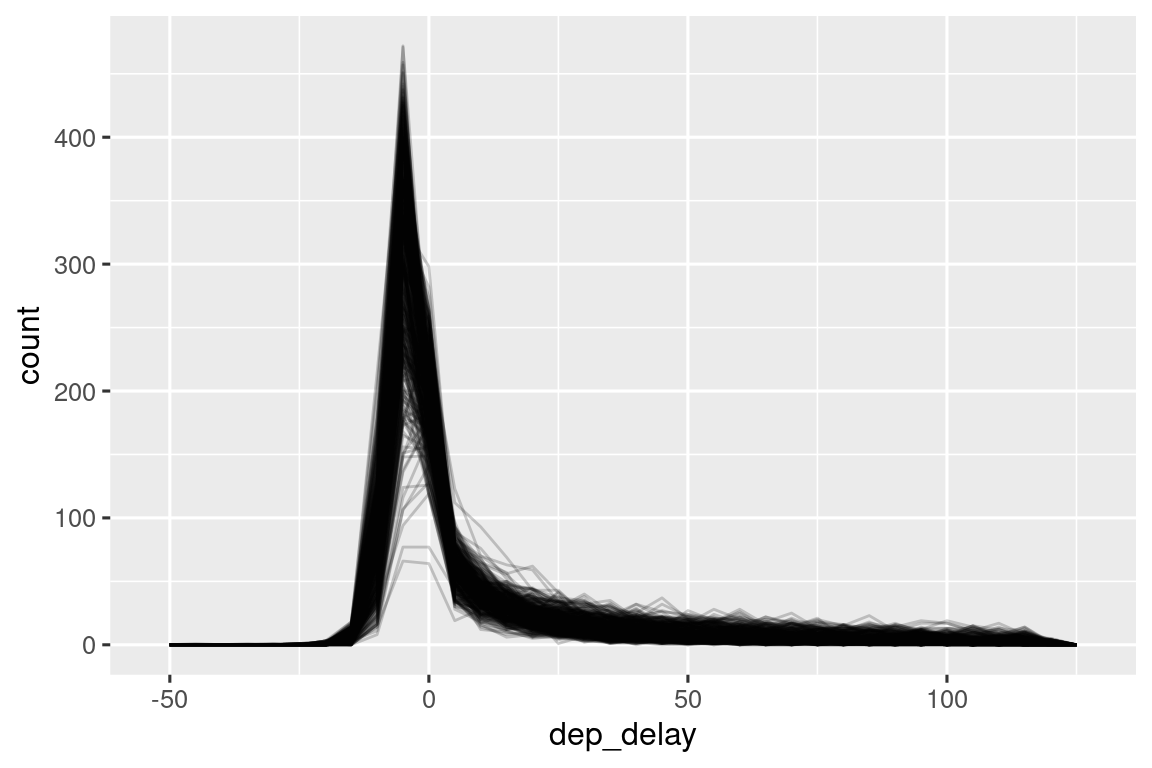

Η κατανομή της `dep_delay` είναι έντονα λοξή από τα δεξιά, με μια έντονη κορυφή ρλαφρώς κάτω από το μηδέν. Τα 365 πολύγωνα συχνοτήτων είναι κυρίως αλληλοεπικαλυτπόμενα μεταξύ τους, σχηματίζοντας μια μαύρη, πυκνή μάζα.

Μην φοβάστε να εξερευνήσετε τις δικές σας συνόψεις που είναι ειδικά προσαρμοσμένες για τα δεδομένα με τα οποία εργάζεστε. Σε αυτήν την περίπτωση, αυτό μπορεί να σημαίνει την δημιουργία ξεχωριστής σύνοψης για τις πτήσεις που αναχώρησαν νωρίς έναντι των πτήσεων που αναχώρησαν αργά ή, δεδομένου ότι οι τιμές είναι τόσο πολύ λοξές, μπορείτε να δοκιμάσετε έναν λογαριθμικό μετασχηματισμό. Τέλος, μην ξεχνάτε τι μάθατε στην Ενότητα 3.6: κάθε φορά που δημιουργείτε αριθμητικές συνόψεις, είναι καλή ιδέα να συμπεριλαμβάνετε και τον αριθμό των παρατηρήσεων σε κάθε ομάδα.

13.6.5 Θέσεις

Υπάρχει ένας τελικός τύπος σύνοψης που είναι χρήσιμος για αριθμητικά διανύσματα, αλλά λειτουργεί επίσης και με κάθε άλλο τύπο τιμής: η εξαγωγή μιας τιμής που βρίσκεται σε μία συγκεκριμένη θέση: first(x), last(x) και nth(x, n).

Για παράδειγμα, μπορούμε να βρούμε την πρώτη, την πέμπτη και την τελευταία αναχώρηση για κάθε ημέρα:

flights |> 
  group_by(year, month, day) |> 
  summarize(
    first_dep = first(dep_time, na_rm = TRUE), 
    fifth_dep = nth(dep_time, 5, na_rm = TRUE),
    last_dep = last(dep_time, na_rm = TRUE)
  )
#> `summarise()` has grouped output by 'year', 'month'. You can override using
#> the `.groups` argument.
#> # A tibble: 365 × 6
#> # Groups:   year, month [12]
#>    year month   day first_dep fifth_dep last_dep
#>   <int> <int> <int>     <int>     <int>    <int>
#> 1  2013     1     1       517       554     2356
#> 2  2013     1     2        42       535     2354
#> 3  2013     1     3        32       520     2349
#> 4  2013     1     4        25       531     2358
#> 5  2013     1     5        14       534     2357
#> 6  2013     1     6        16       555     2355
#> # ℹ 359 more rows

(Σημείωση: Επειδή οι συναρτήσεις της dplyr χρησιμοποιούν το _ για να διαχωρίσουν τα στοιχεία των ονομάτων και των ορισμάτων τους, οι συναρτήσεις αυτές χρησιμοποιούν το na_rm αντί για το na.rm.)

Εάν είστε εξοικειωμένοι με το [, στο οποίο θα επανέλθουμε στην Ενότητα 27.2, ίσως αναρωτηθείτε εάν οι συναρτήσεις αυτές θα σας χρειαστούν. Υπάρχουν τρεις λόγοι: το όρισμα default σας επιτρέπει να παρέχετε μία προεπιλογή εάν δεν υπάρχει η καθορισμένη θέση, το όρισμα order_by σας επιτρέπει να παρακάμψετε τοπικά τη σειρά των γραμμών και το όρισμα na_rm σας επιτρέπει να απορρίψετε τις κενές τιμές.

Η εξαγωγή τιμών βάσει θέσης είναι συμπληρωματική στο φιλτράρισμα στις κατατάξεις. Το φιλτράρισμα σας δίνει όλες τις μεταβλητές, με κάθε παρατήρηση να βρίσκετε σε ξεχωριστή γραμμή:

flights |> 
  group_by(year, month, day) |> 
  mutate(r = min_rank(sched_dep_time)) |> 
  filter(r %in% c(1, max(r)))
#> # A tibble: 1,195 × 20
#> # Groups:   year, month, day [365]
#>    year month   day dep_time sched_dep_time dep_delay arr_time sched_arr_time
#>   <int> <int> <int>    <int>          <int>     <dbl>    <int>          <int>
#> 1  2013     1     1      517            515         2      830            819
#> 2  2013     1     1     2353           2359        -6      425            445
#> 3  2013     1     1     2353           2359        -6      418            442
#> 4  2013     1     1     2356           2359        -3      425            437
#> 5  2013     1     2       42           2359        43      518            442
#> 6  2013     1     2      458            500        -2      703            650
#> # ℹ 1,189 more rows
#> # ℹ 12 more variables: arr_delay <dbl>, carrier <chr>, flight <int>, …

13.6.6 Με την `mutate()`

Όπως υποδηλώνει και το όνομα, οι συναρτήσεις σύνοψης συνήθως πάνε μαζί με την summarize(). Ωστόσο, λόγω των κανόνων ανακύκλωσης που συζητήσαμε στην Ενότητα 13.4.1, μπορούν επίσης να συνδυαστούν αποτελεσματικά και με την mutate(), ειδικά όταν θέλετε να κάνετε κάποιο είδος ομαδικής τυποποίησης. Για παράδειγμα:

Το x / sum(x) υπολογίζει την αναλογία ενός συνόλου.
Το (x - mean(x)) / sd(x) υπολογίζει ένα Z-score (τυποποιημένο με μέσο όρο 0 και τυπική απόκλιση 1).
Το (x - min(x)) / (max(x) - min(x)) τυποποιεί στο εύρος [0, 1].
Το x / first(x) υπολογίζει έναν δείκτη με βάση την πρώτη παρατήρηση.

13.6.7 Ασκήσεις

Σκεφθείτε τουλάχιστον 5 διαφορετικούς τρόπους για να αξιολογήσετε τα τυπικά χαρακτηριστικά καθυστέρησης μιας ομάδας πτήσεων. Πότε είναι χρήσιμη η mean();
Πότε είναι χρήσιμη η median();
Πότε μπορεί να θέλετε να χρησιμοποιήσετε κάτι άλλο;
Θα πρέπει να χρησιμοποιήσετε την καθυστέρηση άφιξης ή την καθυστέρηση αναχώρησης;
Γιατί μπορεί να θέλετε να χρησιμοποιήσετε δεδομένα από την μεταβλητή planes;
Ποιοι προορισμοί παρουσιάζουν τη μεγαλύτερη διακύμανση στην ταχύτητα του αέρα;
Δημιουργήστε ένα διάγραμμα για να εξερευνήσετε περαιτέρω τις περιπέτειες του αεροδρομίου EGE. Μπορείτε να βρείτε αποδείξεις ότι το αεροδρόμιο άλλαξε τοποθεσίες;
Μπορείτε να βρείτε κάποια άλλη μεταβλητή που θα μπορούσε να εξηγήσει τη διαφορά;

13.7 Σύνοψη

Είστε ήδη εξοικειωμένοι με πολλά εργαλεία για την εργασία με αριθμούς και, αφού διαβάσατε αυτό το κεφάλαιο, ξέρετε πλέον πώς να τα χρησιμοποιήσετε στην R. Έχετε μάθει επίσης λίγους χρήσιμους γενικούς μετασχηματισμούς που εφαρμόζονται συνήθως, αλλά όχι αποκλειστικά, σε αριθμητικά διανύσματα, όπως κατατάξεις και ορίσματα μετατόπισης. Τέλος, επεξεργαστήκατε μία σειρά από αριθμητικές συνόψεις και συζητήσατε μερικές από τις στατιστικές προκλήσεις που θα πρέπει να λάβετε υπόψη.

Στα επόμενα δύο κεφάλαια, θα ασχοληθούμε με την εργασία με συμβολοσειρές με το πακέτο stringr. Οι συμβολοσειρές αποτελούν μία μεγάλη θεματική ενότητα κι επομένως έχουν δύο κεφάλαια, ένα για τις βασικές αρχές των συμβολοσειρών, και ένα για τις κανονικές εκφράσεις.

Η ggplot2 παρέχει μερικούς βοηθούς για συνήθεις περιπτώσεις με τις cut_interval(), cut_number() και cut_width(). Η ggplot2 είναι ένα ομολογουμένως περίεργο μέρος για να υπάρχουν αυτές οι συναρτήσεις, αλλά είναι χρήσιμες ως μέρος του υπολογισμού ενός ιστογράμματος και γράφτηκαν πριν από την ύπαρξη οποιουδήποτε άλλου τμήματος του tidyverse.↩︎
Η συνάρτηση mode() κάνει κάτι εντελώς διαφορετικό!↩︎